Kendall tau metric
Kendall tau
The non-parametric correlation coefficient (or measure of association) known as Kendall's tau was first discussed by G.T. Fechner and others about 1900, and was rediscovered (independently) by M.G. Kendall in 1938 [a3], [a4]. In modern use, the term "correlation" refers to a measure of a linear relationship between variates (such as the Pearson product-moment correlation coefficient), while "measure of association" refers to a measure of a monotone relationship between variates (such as Kendall's tau and the Spearman rho metric). For a historical review of Kendall's tau and related coefficients, see [a5].
Underlying the definition of Kendall's tau is the notion of concordance. If 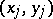 and
and 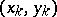 are two elements of a sample
are two elements of a sample 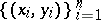 from a bivariate population, one says that
from a bivariate population, one says that 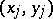 and
and 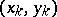 are concordant if
are concordant if 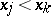 and
and 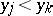 or if
or if 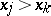 and
and 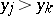 (i.e., if
(i.e., if 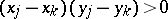 ); and discordant if
); and discordant if 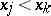 and
and 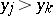 or if
or if 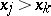 and
and 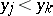 (i.e., if
(i.e., if 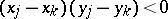 ). There are
). There are 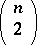 distinct pairs of observations in the sample, and each pair (barring ties) is either concordant or discordant. Denoting by
distinct pairs of observations in the sample, and each pair (barring ties) is either concordant or discordant. Denoting by 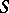 the number
the number  of concordant pairs minus the number
of concordant pairs minus the number  of discordant pairs, Kendall's tau for the sample is defined as
of discordant pairs, Kendall's tau for the sample is defined as
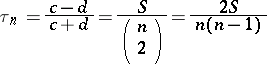 |
When ties exist in the data, the following adjusted formula is used:
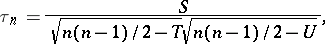 |
where 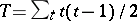 for
for 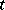 the number of
the number of 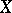 observations that are tied at a given rank, and
observations that are tied at a given rank, and 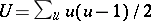 for
for  the number of
the number of 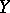 observations that are tied at a given rank. For details on the use of
observations that are tied at a given rank. For details on the use of 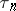 in hypotheses testing, and for large-sample theory, see [a2].
in hypotheses testing, and for large-sample theory, see [a2].
Note that 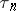 is equal to the probability of concordance minus the probability of discordance for a pair of observations
is equal to the probability of concordance minus the probability of discordance for a pair of observations 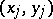 and
and 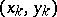 chosen randomly from the sample
chosen randomly from the sample 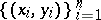 . The population version
. The population version  of Kendall's tau is defined similarly for random variables
of Kendall's tau is defined similarly for random variables 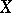 and
and 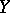 (cf. also Random variable). Let
(cf. also Random variable). Let 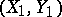 and
and 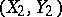 be independent random vectors with the same distribution as
be independent random vectors with the same distribution as 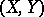 . Then
. Then
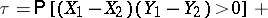 |
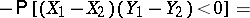 |
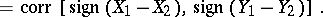 |
Since  is the Pearson product-moment correlation coefficient of the random variables
is the Pearson product-moment correlation coefficient of the random variables 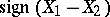 and
and 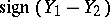 ,
,  is sometimes called the difference sign correlation coefficient.
is sometimes called the difference sign correlation coefficient.
When 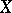 and
and 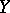 are continuous,
are continuous,
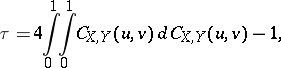 |
where 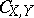 is the copula of
is the copula of 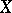 and
and 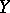 . Consequently,
. Consequently,  is invariant under strictly increasing transformations of
is invariant under strictly increasing transformations of 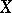 and
and 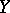 , a property
, a property  shares with Spearman's rho, but not with the Pearson product-moment correlation coefficient. For a survey of copulas and their relationship with measures of association, see [a6].
shares with Spearman's rho, but not with the Pearson product-moment correlation coefficient. For a survey of copulas and their relationship with measures of association, see [a6].
Besides Kendall's tau, there are other measures of association based on the notion of concordance, one of which is Blomqvist's coefficient [a1]. Let 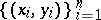 denote a sample from a continuous bivariate population, and let
denote a sample from a continuous bivariate population, and let 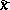 and
and 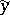 denote sample medians (cf. also Median (in statistics)). Divide the
denote sample medians (cf. also Median (in statistics)). Divide the 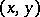 -plane into four quadrants with the lines
-plane into four quadrants with the lines 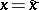 and
and 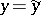 ; and let
; and let 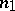 be the number of sample points belonging to the first or third quadrants, and
be the number of sample points belonging to the first or third quadrants, and 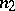 the number of points belonging to the second or fourth quadrants. If the sample size
the number of points belonging to the second or fourth quadrants. If the sample size  is even, the calculation of
is even, the calculation of 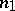 and
and 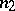 is evident. If
is evident. If  is odd, then one or two of the sample points fall on the lines
is odd, then one or two of the sample points fall on the lines 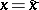 and
and 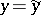 . In the first case one ignores the point; in the second case one assigns one point to the quadrant touched by both points and ignores the other. Then Blomqvist's
. In the first case one ignores the point; in the second case one assigns one point to the quadrant touched by both points and ignores the other. Then Blomqvist's 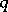 is defined as
is defined as
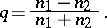 |
For details on the use of 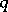 in hypothesis testing, and for large-sample theory, see [a1].
in hypothesis testing, and for large-sample theory, see [a1].
The population parameter estimated by 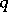 , denoted by
, denoted by 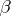 , is defined analogously to Kendall's tau (cf. Kendall tau metric). Denoting by
, is defined analogously to Kendall's tau (cf. Kendall tau metric). Denoting by 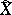 and
and 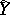 the population medians of
the population medians of 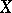 and
and 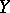 , then
, then
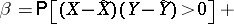 |
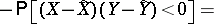 |
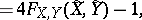 |
where 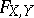 denotes the joint distribution function of
denotes the joint distribution function of 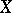 and
and 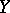 . Since
. Since 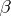 depends only on the value of
depends only on the value of 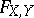 at the point whose coordinates are the population medians of
at the point whose coordinates are the population medians of 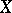 and
and 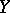 , it is sometimes called the medial correlation coefficient. When
, it is sometimes called the medial correlation coefficient. When 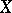 and
and 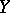 are continuous,
are continuous,
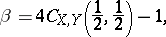 |
where 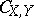 again denotes the copula of
again denotes the copula of 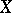 and
and 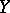 . Thus
. Thus 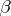 , like
, like  , is invariant under strictly increasing transformations of
, is invariant under strictly increasing transformations of 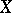 and
and 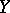 .
.
References
| [a1] | N. Blomqvist, "On a measure of dependence between two random variables" Ann. Math. Stat. , 21 (1950) pp. 503–600 |
| [a2] | J.D. Gibbons, "Nonparametric methods for quantitative analysis" , Holt, Rinehart & Winston (1976) |
| [a3] | M.G. Kendall, "A new measure of rank correlation" Biometrika , 30 (1938) pp. 81–93 |
| [a4] | M.G. Kendall, "Rank correlation methods" , Charles Griffin (1970) (Edition: Fourth) |
| [a5] | W.H. Kruskal, "Ordinal measures of association" J. Amer. Statist. Assoc. , 53 (1958) pp. 814–861 |
| [a6] | R.B. Nelsen, "An introduction to copulas" , Springer (1999) |
Kendall tau metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kendall_tau_metric&oldid=12869