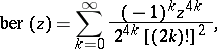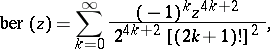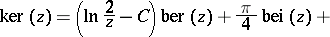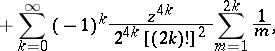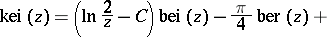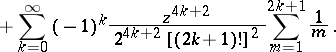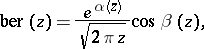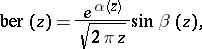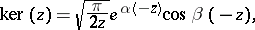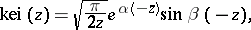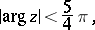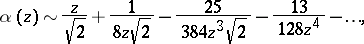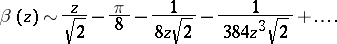Thomson functions
The functions  and
and  ,
,  and
and  ,
,  and
and  , defined by
, defined by
where the  are the Hankel functions and the
are the Hankel functions and the 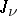 are the Bessel functions. When
are the Bessel functions. When 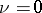 the index is omitted. The Kelvin functions form a fundamental system of solutions of the equation
the index is omitted. The Kelvin functions form a fundamental system of solutions of the equation
which for 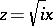 turns into the Bessel equation.
turns into the Bessel equation.
The series representations are:
The asymptotic representations are:
where
These functions were introduced by W. Thomson (Lord Kelvin, [1]).
References
| [1] | W. Thomson, "Mathematical and physical papers" , 3 , Cambridge Univ. Press (1980) pp. 492 |
| [2] | E. Jahnke, F. Emde, F. Lösch, "Tafeln höheren Funktionen" , Teubner (1966) |
| [3] | I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1973) (Translated from Russian) |
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1965) |
How to Cite This Entry:
Kelvin functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kelvin_functions&oldid=15392
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article and
and  ,
,  and
and  ,
,  and
and  , defined by
, defined by
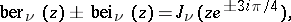
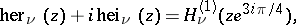
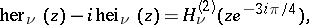
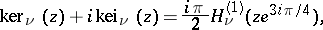
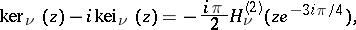
 are the Hankel functions and the
are the Hankel functions and the 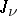 are the Bessel functions. When
are the Bessel functions. When 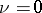 the index is omitted. The Kelvin functions form a fundamental system of solutions of the equation
the index is omitted. The Kelvin functions form a fundamental system of solutions of the equation
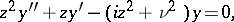
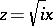 turns into the Bessel equation.
turns into the Bessel equation.