Kellogg-Evans theorem
Kellogg's lemma
The set of all irregular points of the boundary (cf. Irregular boundary point) of an arbitrary domain  in the Euclidean space
in the Euclidean space  ,
,  , with respect to a generalized solution of the Dirichlet problem for
, with respect to a generalized solution of the Dirichlet problem for  in the sense of Wiener–Perron (see Perron method) has capacity zero, is a polar set and has type
in the sense of Wiener–Perron (see Perron method) has capacity zero, is a polar set and has type  (cf. Set of type
(cf. Set of type  (
( )). A corollary of the Kellogg–Evans theorem is that if
)). A corollary of the Kellogg–Evans theorem is that if  is a compact set of positive capacity in
is a compact set of positive capacity in  and
and 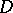 is the connected component of the complement
is the connected component of the complement  containing the point at infinity, then there exists on the boundary
containing the point at infinity, then there exists on the boundary 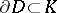 at least one regular point. The Kellogg–Evans theorem was stated by O.D. Kellogg [1] as a conjecture, and was first proved by G.C. Evans [2].
at least one regular point. The Kellogg–Evans theorem was stated by O.D. Kellogg [1] as a conjecture, and was first proved by G.C. Evans [2].
References
| [1] | O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967) |
| [2] | G.C. Evans, "Application of Poincaré's sweeping-out process" Proc. Nat. Acad. Sci. USA , 19 (1933) pp. 457–461 |
| [3] | M.V. Keldysh, "On the solvability and stability of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 171–231 (In Russian) |
| [4] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
Kellogg-Evans theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kellogg-Evans_theorem&oldid=13358