Keisler-Shelah isomorphism theorem
Interpretations for a first-order language 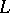 are said to be elementarily equivalent (in
are said to be elementarily equivalent (in 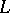 ) provided that they make exactly the same sentences in
) provided that they make exactly the same sentences in 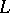 true (cf. also Interpretation). The Keisler–Shelah isomorphism theorem provides a characterization of elementary equivalence: interpretations for
true (cf. also Interpretation). The Keisler–Shelah isomorphism theorem provides a characterization of elementary equivalence: interpretations for 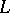 are elementarily equivalent if and only if they have isomorphic ultrapowers (cf. also Ultrafilter).
are elementarily equivalent if and only if they have isomorphic ultrapowers (cf. also Ultrafilter).
This theorem was formulated and proved by H.J. Keisler in 1961 [a2]. Keisler gave a second proof in 1964 using saturated ultrapowers [a3]. Both proofs use the generalized continuum hypothesis (GCH). In 1971 S. Shelah gave a third proof [a5]. This proof avoids the generalized continuum hypothesis.
Given 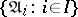 , a non-empty family of interpretations for
, a non-empty family of interpretations for 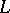 , and
, and 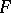 an ultrafilter on
an ultrafilter on 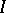 , the ultraproduct
, the ultraproduct 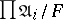 of the family is the quotient system on the direct product of the family induced by
of the family is the quotient system on the direct product of the family induced by 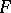 . When there is a fixed interpretation,
. When there is a fixed interpretation, 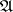 , such that each
, such that each 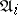 coincides with
coincides with 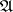 ,
, 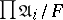 is denoted by
is denoted by 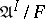 and is called an ultrapower of
and is called an ultrapower of 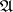 . It follows from results of J. Łos [a4] that
. It follows from results of J. Łos [a4] that 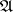 and any of its ultrapowers are elementarily equivalent (the Łos isomorphism theorem). Hence, interpretations with isomorphic ultrapowers are elementarily equivalent.
and any of its ultrapowers are elementarily equivalent (the Łos isomorphism theorem). Hence, interpretations with isomorphic ultrapowers are elementarily equivalent.
Let 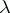 be an infinite cardinal no smaller than the cardinality of the set of sentences in
be an infinite cardinal no smaller than the cardinality of the set of sentences in 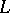 , and let
, and let 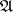 and
and 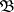 be interpretations for
be interpretations for 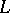 of cardinality less than or equal to
of cardinality less than or equal to 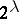 . Let
. Let 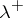 denote the cardinal successor of
denote the cardinal successor of 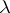 . Keisler showed (assuming that
. Keisler showed (assuming that 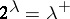 ) that
) that 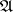 and
and 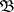 are elementarily equivalent if and only if there are ultrafilters
are elementarily equivalent if and only if there are ultrafilters 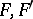 on
on 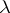 such that
such that 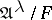 and
and 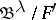 are isomorphic.
are isomorphic.
Let 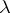 be as above and let
be as above and let 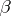 be the least cardinal such that
be the least cardinal such that 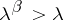 . Shelah showed (without assuming that
. Shelah showed (without assuming that 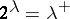 ) that there is an ultrafilter
) that there is an ultrafilter 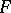 on
on 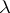 such that, given
such that, given 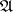 and
and 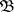 , elementarily equivalent interpretations of cardinality less than
, elementarily equivalent interpretations of cardinality less than 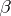 ,
, 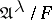 and
and 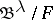 are isomorphic.
are isomorphic.
The motivation for Keisler's results can be found in a programme propounded by A. Tarski [a6]: to provide characterizations of meta-mathematical notions in "purely mathematical terms" . A discussion of this programme and its history can be found in [a7]. To appreciate what was intended here, recall G. Birkhoff's 1935 characterization [a1] of the classes of models of sets of equations (the equational classes): A class of algebras is an equational class if and only if it is closed under subalgebras, homomorphic images and direct products. This result characterizes equational classes without mentioning equations.
Amongst the consequences of the Keisler–Shelah isomorphism theorem is a comparable "mathematical" characterization of the classes of models of sentences in 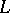 . Given
. Given 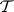 , a class of interpretations for
, a class of interpretations for 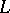 ,
, 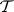 is an elementary class provided that there is a sentence in
is an elementary class provided that there is a sentence in 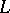 whose models are exactly the members of
whose models are exactly the members of 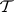 ;
; 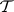 is an elementary class in the wider sense provided that there is a set of sentences in
is an elementary class in the wider sense provided that there is a set of sentences in 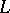 whose models are exactly the members of
whose models are exactly the members of 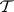 . It follows from the compactness theorem that
. It follows from the compactness theorem that 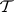 is an elementary class if and only if both
is an elementary class if and only if both 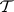 and its complement (relative to the class of interpretations for
and its complement (relative to the class of interpretations for 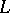 ) are elementary classes in the wider sense. Keisler [a2] showed (assuming GCH) that:
) are elementary classes in the wider sense. Keisler [a2] showed (assuming GCH) that:
1) 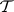 is an elementary class in the wider sense, provided that
is an elementary class in the wider sense, provided that 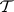 is closed under isomorphic images and ultraproducts and the complement of
is closed under isomorphic images and ultraproducts and the complement of 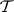 is closed under ultrapowers;
is closed under ultrapowers;
2) 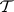 is an elementary class if and only if both
is an elementary class if and only if both 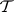 and its complement are closed under isomorphic images and ultraproducts.
and its complement are closed under isomorphic images and ultraproducts.
Whilst Keisler's proof of this result used the generalized continuum hypothesis, its use was restricted to establishing that elementarily equivalent interpretations have isomorphic ultrapowers. Hence, by eliminating GCH in the proof of the latter result, Shelah also eliminated the use of GCH from Keisler's characterization of elementary classes.
References
| [a1] | G. Birkhoff, "On the structure of abstract algebras" Proc. Cambridge Philos. Soc. , 31 (1935) pp. 433–454 |
| [a2] | H.J. Keisler, "Ultraproducts and elementary models" Indagationes Mathematicae , 23 (1961) pp. 477–495 |
| [a3] | H.J. Keisler, "Ultraproducts and saturated classes" Indagationes Mathematicae , 26 (1964) pp. 178–186 |
| [a4] | J. Łos, "Quelques remarqes, théorèmes et problèmes sur les classes définissables d'algèbres" , Mathematical Interpretations of Formal Systems , North-Holland (1955) pp. 98–113 |
| [a5] | S. Shelah, "Every two elementarily equivalent models have isomorphic ultrapowers" Israel J. Math. , 10 (1971) pp. 224–233 |
| [a6] | A. Tarski, "Some notions and methods on the borderline of algebra and metamathematics" , Proc. Intern. Congress of Math. (Cambridge, MA, 1950) , 1 , Amer. Math. Soc. (1952) pp. 705–720 |
| [a7] | R.L. Vaught, "Model theory before 1945" , Proc. Tarski Symp. , Amer. Math. Soc. (1974) pp. 153–172 |
Keisler-Shelah isomorphism theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Keisler-Shelah_isomorphism_theorem&oldid=11976