Kazdan inequality
From Encyclopedia of Mathematics
Let  be a real
be a real 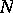 -dimensional scalar inner product space (cf. also Inner product; Pre-Hilbert space), let
-dimensional scalar inner product space (cf. also Inner product; Pre-Hilbert space), let 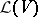 be the space of linear operators of
be the space of linear operators of 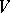 , and let
, and let 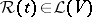 be a given family of symmetric linear operators depending continuously on
be a given family of symmetric linear operators depending continuously on 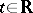 . For
. For 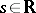 , denote by
, denote by  the solution of the initial value problem
the solution of the initial value problem
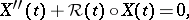 |
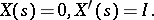 |
Suppose that  is invertible for all
is invertible for all 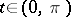 . Then for every positive
. Then for every positive 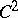 -function
-function 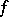 on
on 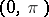 satisfying
satisfying 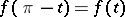 on
on 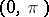 , one has
, one has
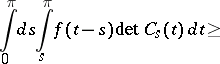 |
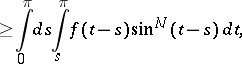 |
with equality if and only if 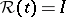 for all
for all 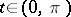 .
.
References
| [a1] | J.L. Kazdan, "An inequality arising in geometry" A.L. Besse (ed.) , Manifolds all of whose Geodesics are Closed , Springer (1978) pp. 243–246; Appendix E |
| [a2] | I. Chavel, "Riemannian geometry: A modern introduction" , Cambridge Univ. Press (1995) |
How to Cite This Entry:
Kazdan inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kazdan_inequality&oldid=17407
Kazdan inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kazdan_inequality&oldid=17407
This article was adapted from an original article by H. Kaul (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article