Kawamata rationality theorem
A theorem stating that there is a strong restriction for the canonical divisor of an algebraic variety to be negative while the positivity is arbitrary. It is closely related to the structure of the cone of curves and the existence of rational curves.
Definitions and terminology.
Let  be a normal algebraic variety (cf. Algebraic variety). A
be a normal algebraic variety (cf. Algebraic variety). A  -divisor
-divisor 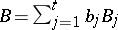 on
on  is a formal linear combination of a finite number of prime divisors
is a formal linear combination of a finite number of prime divisors  of
of  with rational number coefficients
with rational number coefficients  (cf. also Divisor). The canonical divisor
(cf. also Divisor). The canonical divisor  is a Weil divisor on
is a Weil divisor on 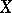 corresponding to a non-zero rational differential
corresponding to a non-zero rational differential  -form for
-form for 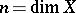 (cf. also Differential form). The pair
(cf. also Differential form). The pair  is said to be weakly log-terminal if the following conditions are satisfied:
is said to be weakly log-terminal if the following conditions are satisfied:
The coefficients of 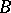 satisfy
satisfy 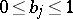 .
.
There exists a positive integer  such that
such that 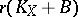 is a Cartier divisor (cf. Divisor).
is a Cartier divisor (cf. Divisor).
There exists a projective birational morphism  from a smooth variety such that the union
from a smooth variety such that the union
 |
is a normal crossing divisor (cf. Divisor), where 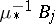 is the strict transform of
is the strict transform of 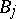 and
and 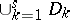 coincides with the smallest closed subset
coincides with the smallest closed subset 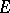 of
of 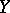 such that
such that 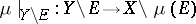 is an isomorphism.
is an isomorphism.
One can write
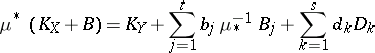 |
such that 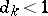 for all
for all  .
.
There exist positive integers 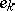 such that the divisor
such that the divisor  is
is  -ample (cf. also Ample vector bundle).
-ample (cf. also Ample vector bundle).
For example, the pair  is weak log-terminal if
is weak log-terminal if  is smooth and
is smooth and 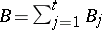 is a normal crossing divisor, or if
is a normal crossing divisor, or if 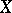 has only quotient singularities and
has only quotient singularities and  .
.
Rationality theorem.
Let 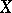 be a normal algebraic variety defined over an algebraically closed field of characteristic
be a normal algebraic variety defined over an algebraically closed field of characteristic  , and let
, and let  be a
be a 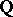 -divisor on
-divisor on  such that the pair
such that the pair 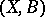 is weakly log-terminal. Let
is weakly log-terminal. Let  be a projective morphism (cf. Projective scheme) to another algebraic variety
be a projective morphism (cf. Projective scheme) to another algebraic variety 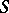 , and let
, and let 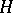 be an
be an 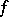 -ample Cartier divisor on
-ample Cartier divisor on  . Then (the rationality theorem, [a1])
. Then (the rationality theorem, [a1])
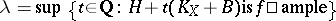 |
is either 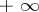 or a rational number. In the latter case, let
or a rational number. In the latter case, let  be the smallest positive integer such that
be the smallest positive integer such that  is a Cartier divisor, and let
is a Cartier divisor, and let  be the maximum of the dimensions of geometric fibres of
be the maximum of the dimensions of geometric fibres of  . Express
. Express 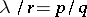 for relatively prime positive integers
for relatively prime positive integers  and
and 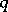 . Then
. Then 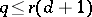 .
.
For example, equality is attained when  ,
, 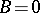 ,
, 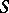 is a point, and
is a point, and  is a hyperplane section.
is a hyperplane section.
The following theorem asserts the existence of a rational curve, a birational image of the projective line 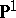 , and provides a more geometric picture. However, the estimate of the denominator
, and provides a more geometric picture. However, the estimate of the denominator 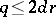 obtained is weaker: In the situation of the above rationality theorem, if
obtained is weaker: In the situation of the above rationality theorem, if 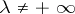 , then there exists a morphism
, then there exists a morphism 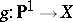 such that
such that 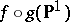 is a point and
is a point and 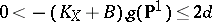 [a2].
[a2].
The two theorems are related in the following way: If 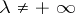 , then
, then 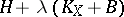 is no longer
is no longer 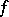 -ample. However, there exists a positive integer
-ample. However, there exists a positive integer 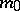 such that the natural homomorphism
such that the natural homomorphism
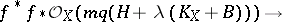 |
 |
is surjective for any positive integer 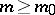 (the base-point-free theorem, [a1]). Let
(the base-point-free theorem, [a1]). Let 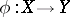 be the associated morphism over the base space
be the associated morphism over the base space 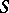 . Then any positive dimensional fibre of
. Then any positive dimensional fibre of 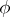 is covered by a family of rational curves as given in the second theorem [a2].
is covered by a family of rational curves as given in the second theorem [a2].
References
| [a1] | Y. Kawamata, K. Matsuda, K. Matsuki, "Introduction to the minimal model problem" , Algebraic Geometry (Sendai 1985) , Adv. Stud. Pure Math. , 10 , Kinokuniya& North-Holland (1987) pp. 283–360 |
| [a2] | Y. Kawamata, "On the length of an extremal rational curve" Invent. Math. , 105 (1991) pp. 609–611 |
Kawamata rationality theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kawamata_rationality_theorem&oldid=16450