Difference between revisions of "Kaplansky field"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> K.A.H. Gravett, "Note on a result of Krull" ''Proc. Cambridge Philos. Soc.'' , '''52''' (1956) pp. 379 {{MR|0075937}} {{ZBL|0073.02702}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I. Kaplansky, "Maximal fields with valuations I" ''Duke Math. J.'' , '''9''' (1942) pp. 303–321 {{MR|6161}} {{ZBL|0061.05506}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Krull, "Allgemeine Bewertungstheorie" ''J. Reine Angew. Math.'' , '''167''' (1932) pp. 160–196 {{MR|}} {{ZBL|0004.09802}} {{ZBL|58.0148.02}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> F.-V. Kuhlmann, M. Pank, P. Roquette, "Immediate and purely wild extensions of valued fields" ''Manuscr. Math.'' , '''55''' (1986) pp. 39–67 {{MR|0828410}} {{ZBL|0593.12018}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> S. Lang, "Algebra" , Addison-Wesley (1974) {{MR|0783636}} {{ZBL|0712.00001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G. Whaples, "Galois cohomology of additive polynomials and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k110/k110020/k11002023.png" />-th power mappings of fields" ''Duke Math. J.'' , '''24''' (1957) pp. 143–150 {{MR|0092826}} {{ZBL|}} </TD></TR></table> |
Revision as of 17:33, 31 March 2012
A field 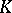 equipped with a valuation
equipped with a valuation  and satisfying Kaplansky's hypothesis A, as introduced in [a2]. Let
and satisfying Kaplansky's hypothesis A, as introduced in [a2]. Let 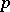 denote the characteristic of the residue field
denote the characteristic of the residue field  if it is a positive prime; otherwise, set
if it is a positive prime; otherwise, set 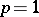 . Hypothesis A requires that:
. Hypothesis A requires that:
i) the value group 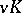 is a
is a 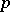 -divisible group;
-divisible group;
ii) for every additive polynomial (cf. [a5])  with coefficients in
with coefficients in 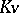 and every
and every 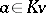 , the equation
, the equation 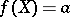 has a solution in
has a solution in 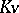 . Requirement ii) implies that
. Requirement ii) implies that 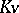 is a perfect field. Using Galois cohomology, G. Whaples [a6] showed that ii) means that the degree of every finite extension of
is a perfect field. Using Galois cohomology, G. Whaples [a6] showed that ii) means that the degree of every finite extension of 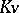 is prime to
is prime to 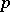 . An elementary proof of this was given by F. Delon in 1981.
. An elementary proof of this was given by F. Delon in 1981.
I. Kaplansky considered immediate extensions (cf. Valuation) of fields with valuations. He used pseudo-Cauchy sequences (also called Ostrowski nets), which were introduced by A. Ostrowski in 1935. These are analogues of Cauchy sequences (cf. Cauchy sequence) for the metric induced by the valuation, but their limits need not be unique; for this reason, they are called pseudo-limits.
In [a3], W. Krull proved that there always exist maximal immediate extensions (in order to apply the Zorn lemma, Krull gave an upper bound for the cardinality of immediate extensions of a fixed field; an elegant deduction of this bound was later given by K.A.H. Gravett in [a1]). Kaplansky showed that if 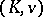 satisfies hypothesis A, then its maximal immediate extensions are unique up to a valuation-preserving isomorphism over
satisfies hypothesis A, then its maximal immediate extensions are unique up to a valuation-preserving isomorphism over 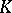 . The same holds for the maximal immediate algebraic extensions, and this fact can also be shown via a Galois-theoretic interpretation of hypothesis A (cf. [a4]). The former result follows from the latter by a theorem of Kaplansky (which has a certain analogue in the theory of real closed fields, cf. Real closed field): If
. The same holds for the maximal immediate algebraic extensions, and this fact can also be shown via a Galois-theoretic interpretation of hypothesis A (cf. [a4]). The former result follows from the latter by a theorem of Kaplansky (which has a certain analogue in the theory of real closed fields, cf. Real closed field): If 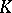 has no non-trivial immediate algebraic extensions, then the isomorphism type of an immediate extension
has no non-trivial immediate algebraic extensions, then the isomorphism type of an immediate extension 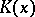 over
over 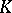 is determined by the pseudo-Cauchy sequences in
is determined by the pseudo-Cauchy sequences in  that have pseudo-limit
that have pseudo-limit  .
.
See also Model theory of valued fields.
References
| [a1] | K.A.H. Gravett, "Note on a result of Krull" Proc. Cambridge Philos. Soc. , 52 (1956) pp. 379 MR0075937 Zbl 0073.02702 |
| [a2] | I. Kaplansky, "Maximal fields with valuations I" Duke Math. J. , 9 (1942) pp. 303–321 MR6161 Zbl 0061.05506 |
| [a3] | W. Krull, "Allgemeine Bewertungstheorie" J. Reine Angew. Math. , 167 (1932) pp. 160–196 Zbl 0004.09802 Zbl 58.0148.02 |
| [a4] | F.-V. Kuhlmann, M. Pank, P. Roquette, "Immediate and purely wild extensions of valued fields" Manuscr. Math. , 55 (1986) pp. 39–67 MR0828410 Zbl 0593.12018 |
| [a5] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [a6] | G. Whaples, "Galois cohomology of additive polynomials and  -th power mappings of fields" Duke Math. J. , 24 (1957) pp. 143–150 MR0092826 -th power mappings of fields" Duke Math. J. , 24 (1957) pp. 143–150 MR0092826 |
Kaplansky field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kaplansky_field&oldid=14681