Difference between revisions of "Kähler manifold"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Kähler manifold to Kaehler manifold: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
A complex manifold which admits a Kähler metric. Sometimes it is called a manifold of Kähler type, with the term "Kähler manifold" being reserved for manifolds actually equipped with a Kähler metric [1]. Any submanifold of a Kähler manifold is a Kähler manifold. In particular, all projective complex algebraic varieties without singular points are Kähler manifolds, and, moreover, their Kähler metric is induced by the Fubini–Study metric on the complex projective space. Similarly, every submanifold in the affine space 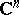 (in particular, every Stein manifold) is a Kähler manifold. Other examples of Kähler manifolds are obtained if one considers the quotient space
(in particular, every Stein manifold) is a Kähler manifold. Other examples of Kähler manifolds are obtained if one considers the quotient space 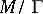 of a Kähler manifold
of a Kähler manifold 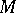 by a discrete group
by a discrete group  of analytic automorphisms preserving the Kähler metric. In particular, every complex torus is a Kähler manifold. Any one-dimensional complex manifold is Kählerian.
of analytic automorphisms preserving the Kähler metric. In particular, every complex torus is a Kähler manifold. Any one-dimensional complex manifold is Kählerian.
The theory of harmonic forms on a compact Kähler manifold  yields the following properties of the de Rham and Dolbeault cohomology groups on
yields the following properties of the de Rham and Dolbeault cohomology groups on 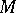 (see [1], [2], and also [5], where these properties were first established for projective algebraic varieties):
(see [1], [2], and also [5], where these properties were first established for projective algebraic varieties):
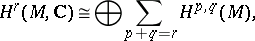 |
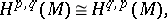 |
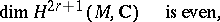 |
 |
Holomorphic forms on a compact Kähler manifold are closed. In particular,
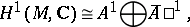 |
where 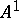 is the space of all holomorphic
is the space of all holomorphic 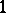 -forms on
-forms on  . If
. If 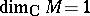 , the number
, the number
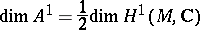 |
is the genus of 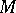 as a compact Riemann surface (cf. also Genus of a surface; Riemann surface). The above properties provide the basis for the construction of examples of non-Kähler compact manifolds, the simplest of which is the Hopf surface, which is diffeomorphic to
as a compact Riemann surface (cf. also Genus of a surface; Riemann surface). The above properties provide the basis for the construction of examples of non-Kähler compact manifolds, the simplest of which is the Hopf surface, which is diffeomorphic to  .
.
A Kähler manifold 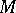 is called a Hodge variety if its Kähler metric is a Hodge metric. Any projective algebraic variety without singular points is a Hodge variety relative to the metric induced by the Fubini–Study metric. Conversely, any compact complex manifold
is called a Hodge variety if its Kähler metric is a Hodge metric. Any projective algebraic variety without singular points is a Hodge variety relative to the metric induced by the Fubini–Study metric. Conversely, any compact complex manifold 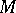 equipped with a Kählerian Hodge metric
equipped with a Kählerian Hodge metric 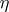 can be biholomorphically imbedded in a complex projective space in such a way that the metric induced on
can be biholomorphically imbedded in a complex projective space in such a way that the metric induced on 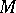 by the Fubini–Study metric may be expressed as
by the Fubini–Study metric may be expressed as 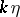 for some natural number
for some natural number 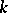 (Kodaira's projective imbedding theorem [1], [3]). Thus, a compact complex manifold
(Kodaira's projective imbedding theorem [1], [3]). Thus, a compact complex manifold 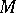 is isomorphic to a projective algebraic variety if and only if it is a Hodge variety. Another form of this criterion: A compact complex manifold
is isomorphic to a projective algebraic variety if and only if it is a Hodge variety. Another form of this criterion: A compact complex manifold 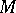 is a projective algebraic variety if and only if it admits a negative vector bundle. Kodaira's theorem can be generalized to complex spaces (see [4], [6]). Compact Kähler manifolds which are not Hodge varieties may be found among the two-dimensional complex tori. For example, this is the case for the torus
is a projective algebraic variety if and only if it admits a negative vector bundle. Kodaira's theorem can be generalized to complex spaces (see [4], [6]). Compact Kähler manifolds which are not Hodge varieties may be found among the two-dimensional complex tori. For example, this is the case for the torus 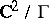 , where
, where 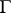 is the lattice spanned by the vectors
is the lattice spanned by the vectors 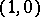 ,
, 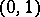 ,
, 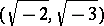 ,
, 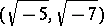 (see [1], [3]). Another necessary and sufficient condition for an
(see [1], [3]). Another necessary and sufficient condition for an  -dimensional compact Kähler manifold
-dimensional compact Kähler manifold 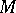 to be projective is that there exist
to be projective is that there exist  algebraically independent meromorphic functions on
algebraically independent meromorphic functions on 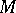 [8].
[8].
Any non-compact complete Kähler manifold with positive sectional curvature is a Stein manifold. The same is true of any simply-connected complete Kähler manifold of non-positive sectional curvature [7].
References
| [1] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [2] | A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958) |
| [3] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [5] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952) |
| [6] | H. Grauert, "Ueber Modifikationen und exzeptionelle analytische Mengen" Math. Ann. , 146 (1962) pp. 331–368 |
| [7] | R.E. Greene, H. Wu, "A theorem in complex geometric function theory" , Value-distribution Theory , A , M. Dekker (1974) pp. 145–167 |
| [8] | B.G. Moishezon, "On  -dimensional compact complex manifolds possessing -dimensional compact complex manifolds possessing  algebraically independent meromorphic functions I - III" Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 133–174; 345–386; 621–656 (In Russian) algebraically independent meromorphic functions I - III" Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 133–174; 345–386; 621–656 (In Russian) |
Comments
A complex compact surface is Kähler if and only if its first Betti number is even.
Let 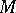 be complex compact manifold of (complex) dimension
be complex compact manifold of (complex) dimension 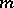 . Let
. Let 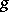 be a Kähler metric on
be a Kähler metric on 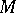 and
and 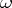 its associated
its associated 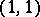 -form. (If
-form. (If 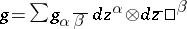 in local coordinates, then
in local coordinates, then 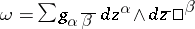 ; giving
; giving 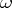 amounts to the same thing as giving
amounts to the same thing as giving 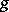 .) Denote by
.) Denote by 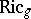 the Ricci curvature tensor of
the Ricci curvature tensor of 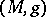 and let
and let 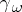 be the associated
be the associated 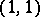 form to
form to 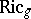 . Then, [a1], the cohomology class of
. Then, [a1], the cohomology class of  is
is 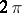 times the first Chern class of
times the first Chern class of 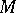 :
: 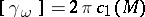 .
.
Now let 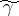 be a given
be a given 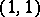 form on
form on 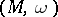 such that
such that 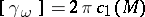 . Then the Calabi conjecture [a2], [a3] states that there is precisely one Kähler form
. Then the Calabi conjecture [a2], [a3] states that there is precisely one Kähler form 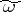 in the same class as
in the same class as 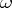 such that
such that 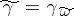 . E. Calabi proved uniqueness.
. E. Calabi proved uniqueness.
A related conjecture is: Let 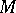 be a complex compact manifold which admits a negative first Chern form. Then there exists a unique Kähler form
be a complex compact manifold which admits a negative first Chern form. Then there exists a unique Kähler form  such that
such that 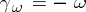 .
.
Such a metric is called an Einstein–Kähler metric. (A Riemannian metric 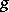 is called an Einstein metric if
is called an Einstein metric if 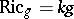 for some constant
for some constant 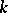 .)
.)
The Calabi conjecture (existence) was proved by S.T. Yau [a4], [a5] and the second conjecture was proved by both T. Aubin and Yau, [a5], [a6].
A Kähler manifold is called a Calabi–Yau manifold if its first Chern class vanishes (so that there exists a Ricci flat on 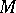 ).
).
These manifolds are of great current interest in theoretical physics as prime candidates for the "missing six dimensions" for a 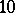 -dimensional super-string theory; i.e. the carrier space of this
-dimensional super-string theory; i.e. the carrier space of this 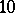 -dimensional space would be
-dimensional space would be 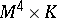 , where
, where  is four-dimensional Minkowski space and
is four-dimensional Minkowski space and 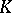 is a six-dimensional ( "small" ) compact Calabi–Yau manifold.
is a six-dimensional ( "small" ) compact Calabi–Yau manifold.
The Calabi–Yau manifolds (with non-vanishing Euler number ( Euler characteristic)) provide the only known "compactifications"
Euler characteristic)) provide the only known "compactifications" 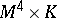 consistent with the super-string equations of motion. A selection of references dealing with these matters is [a8]–[a12].
consistent with the super-string equations of motion. A selection of references dealing with these matters is [a8]–[a12].
References
| [a1] | S.S. Chern, "Characteristic classes of Hermitian manifolds" Ann. of Math. , 47 (1946) pp. 85–121 |
| [a2] | E. Calabi, "The space of Kähler metrics" , Proc. Internat. Congress Mathematicians (Amsterdam, 1954) , 2 , Noordhoff (1954) pp. 206–207 |
| [a3] | E. Calabi, "On Kähler manifolds with vanishing canonical class" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , Algebraic geometry and topology (Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1955) pp. 78–89 |
| [a4] | S.-T. Yau, "On Calabi's conjecture and some new results in algebraic geometry" Proc. Nat. Acad. Sci. USA , 74 (1977) pp. 1798–1799 |
| [a5] | S.-T. Yau, "On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation I" Comm. Pure Appl. Math. , 31 (1978) pp. 339–411 |
| [a6] | T. Aubin, "Equations du type de Monge–Ampère sur les variétés kähleriennes compactes" C.R. Acad. Sci. Paris , 283 (1976) pp. 119–121 |
| [a7] | J.-P. Bourguignon, "Premières formes de Chern des variétés kähleriennes compactes" , Sem. Bourbaki 1977/1978 , Exp. 507 , Springer (1979) pp. 1–21 |
| [a8] | T. Huebsch, "Calabi–Yau manifolds—motivations and constructions" Comm. Math. Phys. , 108 (1987) pp. 291–318 |
| [a9] | M.B. Green, J.H. Schwarz, E. Witten, "Superstring theory" , 2. Loop amplitudes, anomalies & phenomenology , Cambridge Univ. Press (1987) pp. 438ff |
| [a10] | P. Candelas, G. Horowitz, A. Strominger, E. Witten, "Vacuum configurations for superstrings" Nuclear Physics , B258 (1958) pp. 46–74 |
| [a11] | B. de Wit, D.J. Smit, N.D. Hari-Dass, "Residual supersymmetry of compactified 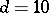 supergravity" Nuclear Physics , B283 (1987) pp. 165–191 supergravity" Nuclear Physics , B283 (1987) pp. 165–191 |
| [a12] | D. Gepner, "Exactly solvable string compactifications on manifolds of 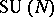 holonomy" Physics Letters , B199 (1987) pp. 380–388 holonomy" Physics Letters , B199 (1987) pp. 380–388 |
| [a13] | "Première classe de Chern et courbure de Ricci: preuve de la conjecture de Calabi" , Sem. Palaiseau 1978 , Soc. Math. France (1978) |
| [a14] | Y.-T. Siu, "Lectures on Hermitean–Einstein metrics for stable bundles and Kähler–Einstein metrics" , Birkhäuser (1987) |
Kähler manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K%C3%A4hler_manifold&oldid=18475