Jump function
One of the three components in the Lebesgue decomposition of a function of bounded variation. Let 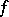 be a function of bounded variation on an interval
be a function of bounded variation on an interval 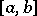 . Let
. Let 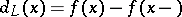 when
when 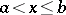 and
and 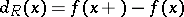 when
when 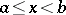 . Then
. Then 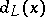 is called the jump of
is called the jump of 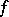 at
at  from the left and
from the left and 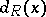 the jump of
the jump of 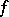 at
at  from the right. If
from the right. If 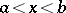 , then
, then
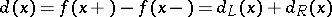 |
is called the jump of 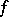 at
at  . Let
. Let 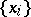 be the sequence of all points of discontinuity of
be the sequence of all points of discontinuity of 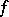 on
on 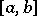 and put
and put
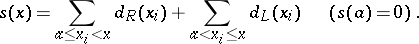 |
Then  is called the jump function of
is called the jump function of 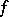 . Note that the difference
. Note that the difference 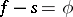 is a continuous function of bounded variation on
is a continuous function of bounded variation on 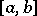 and that
and that 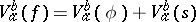 , where
, where 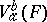 is the variation of
is the variation of  on
on 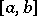 (cf. Variation of a function). Moreover,
(cf. Variation of a function). Moreover,
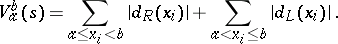 |
References
| [1] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
| [2] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) |
Comments
The function  is also called the saltus function of
is also called the saltus function of 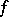 . A function
. A function 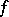 of bounded variation that equals its jump function
of bounded variation that equals its jump function  is itself often called a jump function.
is itself often called a jump function.
References
| [a1] | B. Szökefalvi-Nagy, "Introduction to real functions and orthogonal expansions" , Oxford Univ. Press (1965) |
| [a2] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
Jump function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jump_function&oldid=18207