Julia-Wolff-Carathéodory theorem
Julia–Carathéodory theorem, Julia–Wolff theorem
A classical statement which combines the celebrated Julia theorem from 1920 [a18], Carathéodory's contribution from 1929 [a7] (see also [a8]), and Wolff's boundary version of the Schwarz lemma from 1926 [a30].
Let 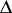 be the open unit disc in the complex plane
be the open unit disc in the complex plane 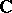 , and let
, and let 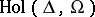 be the set of all holomorphic functions on
be the set of all holomorphic functions on 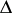 with values in a domain
with values in a domain  in
in 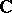 (cf. also Analytic function). For the set
(cf. also Analytic function). For the set 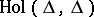 , of holomorphic self-mappings on
, of holomorphic self-mappings on 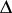 , one writes
, one writes  ; it is a semi-group of holomorphic mappings with respect to composition.
; it is a semi-group of holomorphic mappings with respect to composition.
For 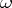 on the unit circle
on the unit circle 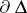 , the boundary of
, the boundary of 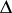 , and
, and 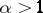 , a non-tangential approach region at
, a non-tangential approach region at 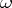 is defined by
is defined by
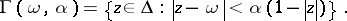 | (a1) |
The term "non-tangential" refers to the fact that at the point 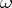 ,
, 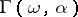 lies in the sector
lies in the sector 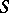 (in
(in 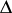 ) that is the region between two straight lines in
) that is the region between two straight lines in 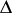 meeting at
meeting at 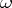 and symmetric about the radius to
and symmetric about the radius to 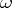 , the boundary curves of
, the boundary curves of 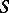 having a corner at
having a corner at 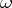 , with angle less than
, with angle less than 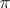 .
.
A function 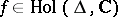 is said to have a non-tangential limit
is said to have a non-tangential limit 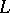 at
at 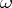 if
if 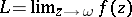 exists in each non-tangential region
exists in each non-tangential region 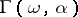 . In this case one also writes
. In this case one also writes
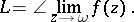 |
For 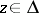 and
and 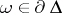 , let
, let
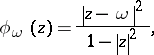 | (a2) |
and for 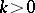 , let
, let
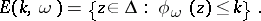 | (a3) |
The set 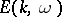 is a closed disc internally tangent to the circle at
is a closed disc internally tangent to the circle at 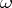 with centre
with centre 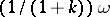 and radius
and radius  . Such a disc is called a horodisc (cf. also Horosphere).
. Such a disc is called a horodisc (cf. also Horosphere).
In 1920, G. Julia [a18] identified hypotheses showing how to get the existence of the non-tangential limit at a given boundary point.
Julia's lemma.
Let 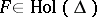 be not constant. Suppose that there are points
be not constant. Suppose that there are points 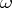 and
and 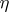 on the boundary
on the boundary 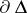 , such that for a sequence
, such that for a sequence 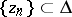 converging to
converging to 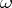 the sequence
the sequence 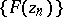 converges to
converges to 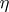 and
and
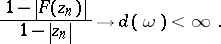 | (a4) |
Then
i) 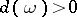 ;
;
ii) 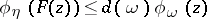 , i.e.
, i.e. 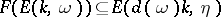 for all
for all 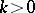 ;
;
iii) 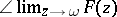 exists and is equal to
exists and is equal to  . Moreover, if the equality in ii) holds for some
. Moreover, if the equality in ii) holds for some 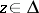 , then
, then 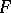 is an automorphism of the disc.
is an automorphism of the disc.
Julia–Carathéodory theorem.
In 1929, C. Carathéodory [a7] proved that under Julia's hypotheses the derivative also admits a non-tangential limit at the same boundary point.
Suppose 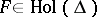 . Then the following statements are equivalent:
. Then the following statements are equivalent:
i) 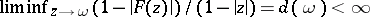 , where the limit is taken as
, where the limit is taken as  approaches
approaches 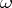 unrestrictedly in
unrestrictedly in 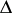 ;
;
ii) 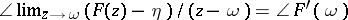 exists for some
exists for some 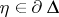 ;
;
iii) 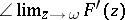 exists, and
exists, and 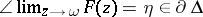 . Moreover,
. Moreover,
a) 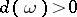 in i);
in i);
b) the boundary points 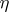 in ii) and iii) are the same;
in ii) and iii) are the same;
c) 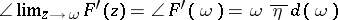 .
.
After appropriate preliminary rotations, one may assume that 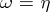 . Thus, these results show that if
. Thus, these results show that if 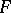 has an angular derivative at some boundary point
has an angular derivative at some boundary point 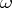 such that
such that
 |
then 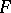 cannot have an interior fixed point in
cannot have an interior fixed point in 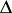 .
.
Now assume only that 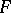 has no interior fixed point in
has no interior fixed point in 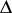 . The question then is: Does the angular derivative at a certain point on the boundary exist?
. The question then is: Does the angular derivative at a certain point on the boundary exist?
The affirmative answer was given by J. Wolff [a30] in 1926.
Wolff's theorem.
Suppose 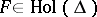 has no fixed point in
has no fixed point in 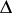 . Then there is a unique unimodular point
. Then there is a unique unimodular point 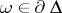 such that
such that
i) 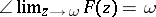 ;
;
ii) 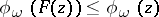 ;
;
iii) 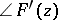 exists and is less than or equal to
exists and is less than or equal to 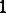 .
.
The latter assertion can be interpreted as a direct analogue of the Schwarz–Pick lemma (cf. Schwarz lemma), where the role of the fixed point is taken over by a point on the unit circle. Moreover, this result is the key to all the deeper facts about sequences of iterates.
Generalizations.
There are various versions and proofs of the Julia–Carathéodory theorem (sometimes also called the Julia–Wolff–Carathéodory theorem or Julia–Wolff theorem). For the one-dimensional case, see, for example, [a19], [a29], [a27], [a12], [a26], [a6], [a21] or [a8], [a22], [a28], [a9].
Note that D. Sarason [a26] gave an interesting proof of the Julia–Carathéodory theorem by using Hilbert space constructions for angular derivatives.
A strengthened version of Julia's lemma was established by P.R. Mercer [a21], employing techniques for the hyperbolic Poincaré metric (cf. Poincaré model).
Different generalizations of the Julia–Wolff–Carathéodory theorem for bounded domains in 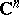 are known: for the unit ball in
are known: for the unit ball in 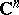 ([a16], [a25]), for the poly-disc ([a17], [a4]), for strongly convex and strongly pseudo-convex domains ([a2], [a3]). Also, M. Abate and R. Tauraso [a1] have described a general framework allowing one to generalize the Julia–Wolff–Carathéodory theorem in terms of the Kobayashi metric (cf. also Hyperbolic metric; Kobayashi hyperbolicity) on a bounded domain in
([a16], [a25]), for the poly-disc ([a17], [a4]), for strongly convex and strongly pseudo-convex domains ([a2], [a3]). Also, M. Abate and R. Tauraso [a1] have described a general framework allowing one to generalize the Julia–Wolff–Carathéodory theorem in terms of the Kobayashi metric (cf. also Hyperbolic metric; Kobayashi hyperbolicity) on a bounded domain in  .
.
For generalizations of Wolff's theorem in the unit ball of a complex Hilbert space, see [a13] and [a14].
Earlier, V.P. Potapov [a23] extended Julia's lemma to matrix-valued holomorphic mappings of a complex variable. His results, as well as the Julia–Wolff–Carathéodory theorem, were generalized by K. Fan and T. Ando ([a10], [a11] and [a5]) to operator-valued holomorphic mappings. Also, in these works they extended the Julia–Wolff–Carathéodory theorem to holomorphic mappings of proper contractions on the unit Hilbert ball acting in the sense of functional calculus.
K. Wlodarczyk [a31] and P. Mellon [a20] have presented some more general results in this direction for the holomorphic mappings on the open unit ball of so-called 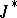 -algebras, using techniques developed by L.A. Harris [a15].
-algebras, using techniques developed by L.A. Harris [a15].
For a survey of work in higher dimensions, see [a25], [a14], [a9], [a24], [a20], [a1].
References
| [a1] | M. Abate, R. Tauraso, "The Julia–Wolff–Caratheodory theorem(s)" Contemp. Math. , 222 (1999) pp. 161–172 |
| [a2] | M. Abate, "The Lindelöf principle and the angular derivative in strongly convex domains" J. Anal. Math. , 54 (1990) pp. 189–228 |
| [a3] | M. Abate, "Angular derivatives in strongly pseudoconvex domains" , Proc. Symp. Pure Math. , 52/2 , Amer. Math. Soc. (1991) pp. 23–40 |
| [a4] | M. Abate, "The Julia–Wolff–Caratheodory theorem in polydisks" J. Anal. Math. , 74 (1998) |
| [a5] | T. Ando, K. Fan, "Pick–Julia theorems for operators" Math. Z. , 168 (1979) pp. 23–34 |
| [a6] | R.B. Burckel, "Iterating analytic self-maps of discs" Amer. Math. Monthly , 88 (1981) pp. 396–407 |
| [a7] | C. Caratheodory, "Uber die Winkelderivierten von beschränkten Analytischen Funktionen" Sitzungsber. Preuss. Akad. Wiss. Berlin, Phys.-Math. Kl. (1929) pp. 39–54 |
| [a8] | C. Caratheodory, "Theory of functions of a complex variable" , Chelsea (1954) |
| [a9] | C.C. Cowen, B.D. MacCluer, "Composition operators on spaces of analytic functions" , CRC (1995) |
| [a10] | K. Fan, "Julia's lemma for operators" Math. Ann. , 239 (1979) pp. 241–245 |
| [a11] | K. Fan, "Iterations of analytic functions of operators" Math. Z. , 179 (1982) pp. 293–298 |
| [a12] | J.L. Goldberg, "Functions with positive real part in a half-plane" Duke Math. J. , 29 (1962) pp. 335–339 |
| [a13] | K. Goebel, "Fixed points and invariant domains of holomorphic mappings of the Hilbert ball" Nonlin. Anal. , 6 (1982) pp. 1327–1334 |
| [a14] | K. Goebel, S. Reich, "Uniform convexity, hyperbolic geometry and nonexpansive mappings" , M. Dekker (1984) |
| [a15] | L.A. Harris, "Bounded symmetric homogeneous domains in infinite-dimensional space" , Lecture Notes in math. , 364 , Springer (1974) pp. 13–40 |
| [a16] | M. Hervé, "Quelques propriétés des applications analytiques d'une boule á 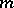 dimensions dans elle-même" J. Math. Pures Appl. , 42 (1963) pp. 117–147 dimensions dans elle-même" J. Math. Pures Appl. , 42 (1963) pp. 117–147 |
| [a17] | F. Jafari, "Angular derivatives in polydisks" Indian J. Math. , 35 (1993) pp. 197–212 |
| [a18] | G. Julia, "Extension nouvelle d'un lemme de Schwarz" Acta Math. , 42 (1920) pp. 349–355 |
| [a19] | E. Landau, G. Valiron, "A deduction from Schwarz's lemma" J. London Math. Soc. , 4 (1929) pp. 162–163 |
| [a20] | P. Mellon, "Another look at results of Wolff and Julia type for 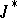 -algebras" J. Math. Anal. Appl. , 198 (1996) pp. 444–457 -algebras" J. Math. Anal. Appl. , 198 (1996) pp. 444–457 |
| [a21] | P.R. Mercer, "On a strengthened Schwarz–Pick inequality" J. Math. Anal. Appl. , 234 (1999) pp. 735–739 |
| [a22] | R. Nevanlinna, "Analytic functions" , Springer (1970) |
| [a23] | V.P. Potapov, "The multiplicative study of 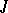 -contractive matrix functions" Amer. Math. Soc. Transl. (2) , 15 (1960) pp. 231–243 -contractive matrix functions" Amer. Math. Soc. Transl. (2) , 15 (1960) pp. 231–243 |
| [a24] | S. Reich, D. Shoikhet, "The Denjoy–Wolff theorem" Ann. Univ. Mariae Curie–Skłodowska , 51 (1997) pp. 219–240 |
| [a25] | W. Rudin, "Function theory on the unit ball in  " , Springer (1980) " , Springer (1980) |
| [a26] | D. Sarason, "Angular derivatives via Hilbert space" Complex Variables , 10 (1988) pp. 1–10 |
| [a27] | J. Serrin, "A note on harmonic functions defined in a half-plane" Duke Math. J. , 23 (1956) pp. 523–526 |
| [a28] | J.H. Shapiro, "Composition operators and classical function theory" , Springer (1993) |
| [a29] | G. Valiron, "Sur l'iteration des fonctions holomorphes dans un demi-plan" Bull. Sci. Math. , 55 : 2 (1931) pp. 105–128 |
| [a30] | J. Wolff, "Sur une generalisation d'un theoreme de Schwarz" C.R. Acad. Sci. , 182 (1926) pp. 918–920 |
| [a31] | K. Wlodarczyk, "Julia's lemma and Wolff's theorem for  -algebras" Proc. Amer. Math. Soc. , 99 : 3 (1987) pp. 472–476 -algebras" Proc. Amer. Math. Soc. , 99 : 3 (1987) pp. 472–476 |
Julia-Wolff-Carathéodory theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Julia-Wolff-Carath%C3%A9odory_theorem&oldid=12290