Jordan-Hölder theorem
If a group has a composition series (cf. Composition sequence), then any two of its composition series are isomorphic. C. Jordan [1], [2] and O. Hölder [3] investigated permutation groups in connection with the problem of the solvability of equations by radicals (see Galois theory). Jordan introduced the concepts of composition and chief series (cf. Principal series) for such groups and proved that the indices of two series of the same type (that is, the indices of the subgroups 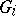 in
in 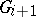 ) are the same, apart from their order of appearance. In other words, it was proved that the sequence of orders of quotients of two composition (chief) series are the same up to a permutation. Hölder proved that the corresponding factors are isomorphic. O. Schreier [4] proved a still stronger assertion: Every two normal series of an arbitrary group have isomorphic refinements (Schreier's theorem). The Jordan–Hölder theorem has also been proved for groups with operators (E. Noether, W. Krull), whence follow the analogous theorems for invariant and fully-invariant series.
) are the same, apart from their order of appearance. In other words, it was proved that the sequence of orders of quotients of two composition (chief) series are the same up to a permutation. Hölder proved that the corresponding factors are isomorphic. O. Schreier [4] proved a still stronger assertion: Every two normal series of an arbitrary group have isomorphic refinements (Schreier's theorem). The Jordan–Hölder theorem has also been proved for groups with operators (E. Noether, W. Krull), whence follow the analogous theorems for invariant and fully-invariant series.
Later generalizations of the Jordan–Hölder theorem went in the following directions. 1) Generalizations of the theorems of Schreier and Jordan–Hölder were obtained for infinite normal systems, and in particular for totally ordered normal and composition series; it was also proved that all ascending normal series of groups with simple factors are isomorphic (these series need not be composition series) (see [5]). 2) The Jordan–Hölder theorem was extended to series of ideals in rings and other algebraic structures. These directions were united by a series of results for  -groups (multi-operator groups),
-groups (multi-operator groups),  -algebras and for universal algebras with a singleton subalgebra and permutable congruences (see [6]–[8]). 3) Various ways of generalizing the Jordan–Hölder theorem have been considered in the language of lattice theory and partially ordered sets. A generalization of Schreier's theorem has been obtained for chains of elements of Dedekind lattices. In a series of papers (see [6], [9]–[11]), an additional relation of normality or an operation of multiplication were introduced in order to define a normal series of elements in a lattice. 4) Generalizations of the Schreier and Jordan–Hölder theorems have been obtained for normal categories (see [8]).
-algebras and for universal algebras with a singleton subalgebra and permutable congruences (see [6]–[8]). 3) Various ways of generalizing the Jordan–Hölder theorem have been considered in the language of lattice theory and partially ordered sets. A generalization of Schreier's theorem has been obtained for chains of elements of Dedekind lattices. In a series of papers (see [6], [9]–[11]), an additional relation of normality or an operation of multiplication were introduced in order to define a normal series of elements in a lattice. 4) Generalizations of the Schreier and Jordan–Hölder theorems have been obtained for normal categories (see [8]).
References
| [1] | C. Jordan, "Théorème sur les équations algébriques" C.R. Acad. Sci. Paris , 68 (1869) pp. 257–258 |
| [2] | C. Jordan, "Traité des substitutions et des équations algébriques" , Paris (1870) pp. 114–125 |
| [3] | O. Hölder, "Zurückführung einer beliebigen algebraischen Gleichung auf eine Kette von Gleichungen" Math. Ann. , 34 (1889) pp. 26–56 |
| [4] | O. Schreier, "Ueber den Jordan–Hölderschen Satz" Abh. Math. Sem. Univ. Hamburg , 6 : 3–4 (1928) pp. 300–302 |
| [5] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [6] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [7] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [8] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
| [9] | Itogi. Nauk. Algebra. 1964 (1966) pp. 237–274 |
| [10] | Itogi Nauk. Algebra. Topol. Geom. 1966 (1968) pp. 109–136 |
| [11] | T.S. Fofanova, "Free extensions of partial polygons" , Ordered sets and lattices , 2 , Saratov (1974) pp. 99–108 (In Russian) |
Comments
References
| [a1] | M. Hall jr., "The theory of groups" , Chelsea, reprint (1976) |
Jordan-Hölder theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan-H%C3%B6lder_theorem&oldid=13194