Joint distribution
A general term referring to the distribution of several random variables defined on the same probability space. Let  be random variables defined on a probability space
be random variables defined on a probability space  and taking values in measurable spaces (cf. Measurable space)
and taking values in measurable spaces (cf. Measurable space)  . The joint distribution of these variables is the function
. The joint distribution of these variables is the function  of sets
of sets  , defined by
, defined by
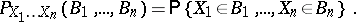 |
In connection with joint distributions, one speaks of the joint distribution function and of the joint probability density.
If  are ordinary real random variables, then their joint distribution is the distribution of the random vector
are ordinary real random variables, then their joint distribution is the distribution of the random vector  in
in  -dimensional Euclidean space
-dimensional Euclidean space 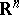 (see Multi-dimensional distribution). If
(see Multi-dimensional distribution). If 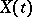 ,
, 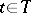 , is a stochastic process, then the joint distributions of the variables
, is a stochastic process, then the joint distributions of the variables 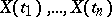 for
for 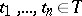 are called the finite-dimensional distributions of the stochastic process
are called the finite-dimensional distributions of the stochastic process 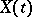 .
.
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
Comments
References
| [a1] | P. Billingsley, "Probability and measure" , Wiley (1979) |
| [a2] | J.L. Doob, "Stochastic processes" , Wiley (1953) |
Joint distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Joint_distribution&oldid=13976