Difference between revisions of "Jaeger composition product"
(Importing text file) |
m (Automatically changed introduction) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 48 formulas, 45 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|part}} | ||
A formula for the [[Jones–Conway polynomial|Jones–Conway polynomial]], describing it as a sum of products of the Jones–Conway polynomials of pieces of the diagram. It has its root in the statistical mechanics model of the Jones–Conway polynomial by V.F.R. Jones. It has been applied to periodic links and to the building of a [[Hopf algebra|Hopf algebra]] structure on the Jones–Conway [[Skein module|skein module]] of the product of a surface and an interval [[#References|[a3]]], [[#References|[a4]]], [[#References|[a2]]]. | A formula for the [[Jones–Conway polynomial|Jones–Conway polynomial]], describing it as a sum of products of the Jones–Conway polynomials of pieces of the diagram. It has its root in the statistical mechanics model of the Jones–Conway polynomial by V.F.R. Jones. It has been applied to periodic links and to the building of a [[Hopf algebra|Hopf algebra]] structure on the Jones–Conway [[Skein module|skein module]] of the product of a surface and an interval [[#References|[a3]]], [[#References|[a4]]], [[#References|[a2]]]. | ||
To define the Jaeger composition product it is convenient to work with the following regular isotopy variant of the Jones–Conway polynomial: | To define the Jaeger composition product it is convenient to work with the following regular isotopy variant of the Jones–Conway polynomial: | ||
| − | + | \begin{equation*} Q _ { D } ( v , z ) = z ^ { \operatorname { com } ( D ) - 1 } v ^ { - \operatorname { Tait } ( D ) } ( v ^ { - 1 } - v ) P _ { D } ( v , z ), \end{equation*} | |
| − | where | + | where $\operatorname { com }( D )$ is the number of link components and $\operatorname{Tait}( D )$ is the algebraic sum of the signs of the crossings of $D$. It is also convenient to add the empty link, $\emptyset$, to the set of links and put $Q _ { \emptyset } ( v , z ) = 1$. $Q _ { D } ( v , z )$ satisfies the skein relation |
| − | + | \begin{equation*} Q _ { D _ { + } } - Q _ { D _ { - } } = \left\{ \begin{array} { l } { Q _ { D _ { 0 } } } \text{ for a self}\square\text{ crossing}, \\ { z ^ { 2 } Q _ { D _ { 0 } } }\text{ for a mixed crossing}, \end{array} \right. \end{equation*} | |
| − | and | + | and $Q _ { D \cup 0 } = ( v ^ { - 1 } - v ) Q _ { D }$. The advantage of working with $Q _ { D } ( v , z )$ is that $Q _ { D } ( v , z ) \in \mathbf{Z} [ v ^ { \pm 1 } , z ^ { 2 } ]$ (no negative powers of $z$) and that the Jaeger composition product has a nice simple form. Indeed ([[#References|[a1]]]): Let $D$ be a diagram of an oriented link in $S ^ { 3 }$, then |
| − | + | \begin{equation*} Q _ { D } ( v _ { 1 } v _ { 2 } , z ) = \sum _ { f \in \text{lbl} ( D ) } \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130010/j13001016.png"/></td> </tr></table> |
| − | The meaning of the used symbols is as follows. To define | + | The meaning of the used symbols is as follows. To define $\operatorname{lbl} ( D )$, consider $D$ as a $4$-valent graph. Let $\operatorname{Edge}( D )$ denote the set of edges of the graph $D$. A $2$-labelling of $D$ is a function $f : \text { Edge } ( D ) \rightarrow \{ 1,2 \}$ such that around a vertex the following labellings are allowed: |
| − | <img | + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/j130010a.gif" style="border:1px solid;"/> |
Figure: j130010a | Figure: j130010a | ||
| − | The set of | + | The set of $2$-labellings of $D$ is denoted by $\operatorname{lbl} ( D )$. The edges of $D$ with label $i$ form an oriented link diagram, denoted by $D _ { f , i }$. The vertices of $D$ which are neither in $D _{f , 1}$ nor $D_{f , 2}$ are called $f$-smoothing vertices of $D$. Let $| f | _ { - }$ (respectively, $| f |_{ +}$) denote the number of negative (respectively, positive) $f$-smoothing vertices of $D$. Let $| f | = | f |_{ -} + | f |_{+}$ and define $\langle D | f \rangle = ( - 1 ) ^ { | f | } - z ^{ | f | - \operatorname { com } ( D _ { f , 1 } ) - \operatorname { com } ( D _ { f , 2 } ) + \operatorname { com } ( D )}$. Finally, $\operatorname{rot} ( D )$ denotes the rotational number of $D$, i.e. the sum of the signs of the Seifert circles of $D$, where the sign of such a circle is $1$ if it is oriented counterclockwise and $- 1$ otherwise. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> F. Jaeger, "Composition products and models for the Homfly polynomial" ''L'Enseign. Math.'' , '''35''' (1989) pp. 323–361</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J.H. Przytycki, "Quantum group of links in a handlebody" M. Gerstenhaber (ed.) J.D. Stasheff (ed.) , ''Deformation Theory and Quantum Groups with Applications to Mathematical Physics'' , ''Contemp. Math.'' , '''134''' (1992) pp. 235–245</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J.H. Przytycki, "A simple proof of the Traczyk–Yokota criteria for periodic knots" ''Proc. Amer. Math. Soc.'' , '''123''' (1995) pp. 1607–1611</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> V.G. Turaev, "Skein quantization of Poisson algebras of loops on surfaces" ''Ann. Sci. Ecole Norm. Sup.'' , '''4''' : 24 (1991) pp. 635–704</td></tr></table> |
Revision as of 17:46, 1 July 2020
A formula for the Jones–Conway polynomial, describing it as a sum of products of the Jones–Conway polynomials of pieces of the diagram. It has its root in the statistical mechanics model of the Jones–Conway polynomial by V.F.R. Jones. It has been applied to periodic links and to the building of a Hopf algebra structure on the Jones–Conway skein module of the product of a surface and an interval [a3], [a4], [a2].
To define the Jaeger composition product it is convenient to work with the following regular isotopy variant of the Jones–Conway polynomial:
\begin{equation*} Q _ { D } ( v , z ) = z ^ { \operatorname { com } ( D ) - 1 } v ^ { - \operatorname { Tait } ( D ) } ( v ^ { - 1 } - v ) P _ { D } ( v , z ), \end{equation*}
where $\operatorname { com }( D )$ is the number of link components and $\operatorname{Tait}( D )$ is the algebraic sum of the signs of the crossings of $D$. It is also convenient to add the empty link, $\emptyset$, to the set of links and put $Q _ { \emptyset } ( v , z ) = 1$. $Q _ { D } ( v , z )$ satisfies the skein relation
\begin{equation*} Q _ { D _ { + } } - Q _ { D _ { - } } = \left\{ \begin{array} { l } { Q _ { D _ { 0 } } } \text{ for a self}\square\text{ crossing}, \\ { z ^ { 2 } Q _ { D _ { 0 } } }\text{ for a mixed crossing}, \end{array} \right. \end{equation*}
and $Q _ { D \cup 0 } = ( v ^ { - 1 } - v ) Q _ { D }$. The advantage of working with $Q _ { D } ( v , z )$ is that $Q _ { D } ( v , z ) \in \mathbf{Z} [ v ^ { \pm 1 } , z ^ { 2 } ]$ (no negative powers of $z$) and that the Jaeger composition product has a nice simple form. Indeed ([a1]): Let $D$ be a diagram of an oriented link in $S ^ { 3 }$, then
\begin{equation*} Q _ { D } ( v _ { 1 } v _ { 2 } , z ) = \sum _ { f \in \text{lbl} ( D ) } \end{equation*}
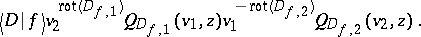 |
The meaning of the used symbols is as follows. To define $\operatorname{lbl} ( D )$, consider $D$ as a $4$-valent graph. Let $\operatorname{Edge}( D )$ denote the set of edges of the graph $D$. A $2$-labelling of $D$ is a function $f : \text { Edge } ( D ) \rightarrow \{ 1,2 \}$ such that around a vertex the following labellings are allowed:

Figure: j130010a
The set of $2$-labellings of $D$ is denoted by $\operatorname{lbl} ( D )$. The edges of $D$ with label $i$ form an oriented link diagram, denoted by $D _ { f , i }$. The vertices of $D$ which are neither in $D _{f , 1}$ nor $D_{f , 2}$ are called $f$-smoothing vertices of $D$. Let $| f | _ { - }$ (respectively, $| f |_{ +}$) denote the number of negative (respectively, positive) $f$-smoothing vertices of $D$. Let $| f | = | f |_{ -} + | f |_{+}$ and define $\langle D | f \rangle = ( - 1 ) ^ { | f | } - z ^{ | f | - \operatorname { com } ( D _ { f , 1 } ) - \operatorname { com } ( D _ { f , 2 } ) + \operatorname { com } ( D )}$. Finally, $\operatorname{rot} ( D )$ denotes the rotational number of $D$, i.e. the sum of the signs of the Seifert circles of $D$, where the sign of such a circle is $1$ if it is oriented counterclockwise and $- 1$ otherwise.
References
| [a1] | F. Jaeger, "Composition products and models for the Homfly polynomial" L'Enseign. Math. , 35 (1989) pp. 323–361 |
| [a2] | J.H. Przytycki, "Quantum group of links in a handlebody" M. Gerstenhaber (ed.) J.D. Stasheff (ed.) , Deformation Theory and Quantum Groups with Applications to Mathematical Physics , Contemp. Math. , 134 (1992) pp. 235–245 |
| [a3] | J.H. Przytycki, "A simple proof of the Traczyk–Yokota criteria for periodic knots" Proc. Amer. Math. Soc. , 123 (1995) pp. 1607–1611 |
| [a4] | V.G. Turaev, "Skein quantization of Poisson algebras of loops on surfaces" Ann. Sci. Ecole Norm. Sup. , 4 : 24 (1991) pp. 635–704 |
Jaeger composition product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jaeger_composition_product&oldid=18470