Jacobson category
An abstract model of the category of Jacobson-commutative algebras (cf. Commutative algebra). It is a special instance of a Zariski category. To be precise, it a Zariski category in which all objects are Jacobson objects, i.e., objects whose prime congruences are meets of maximal congruences. Jacobson categories are axiomatically defined as categories  satisfying the following five axioms:
satisfying the following five axioms:
1)  is co-complete, i.e., has all small colimits;
is co-complete, i.e., has all small colimits;
2)  has a strong generating set of objects whose objects are finitely presentable and directly co-disjunctable;
has a strong generating set of objects whose objects are finitely presentable and directly co-disjunctable;
3) regular epimorphisms in  are universal, i.e., stable under pull-backs along any morphism (cf. also Morphism);
are universal, i.e., stable under pull-backs along any morphism (cf. also Morphism);
4) the terminal object of  is finitely presentable and has no proper subobject;
is finitely presentable and has no proper subobject;
5) the product of two objects in  is co-universal, i.e., stable under pushouts along any morphism.
is co-universal, i.e., stable under pushouts along any morphism.
The notion of a directly co-disjunctable object used in 2) is defined as follows. A morphism  in
in  is a direct factor morphism if there is a morphism
is a direct factor morphism if there is a morphism  in
in  such that
such that 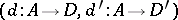 is a product of objects in
is a product of objects in 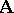 . An object
. An object 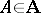 is directly co-disjunctable if the pair of inductions
is directly co-disjunctable if the pair of inductions 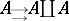 of
of 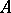 into its coproduct by itself has a co-disjunctor (cf. Zariski category) that is a direct factor morphism.
into its coproduct by itself has a co-disjunctor (cf. Zariski category) that is a direct factor morphism.
What makes Jacobson categories special is the fact that co-disjunctors are co-equalizers or, more concretely, that algebras of fractions are quotient algebras. It follows that integral or local reduced algebras are fields, that reduced algebras are von Neumann regular (cf. also Regular ring (in the sense of von Neumann)), that prime ideals are maximal, that prime spectra are Hausdorff and Boolean spaces, that the set of finitely generated ideals of an algebra is equipped with, next to the usual addition and multiplication of ideals, an extra multiplication of ideals, giving it the structure of a Stone semi-algebra, etc.
A typical example of a Jacobson category is the category  of algebraic commutative algebras over a commutative ring
of algebraic commutative algebras over a commutative ring 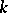 (cf. also Algebraic algebra), i.e., algebras whose elements are algebraic over
(cf. also Algebraic algebra), i.e., algebras whose elements are algebraic over 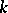 . More generally, the category of algebraic objects of any Zariski category
. More generally, the category of algebraic objects of any Zariski category 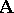 is a Jacobson category, and is indeed the universal Jacobson category associated to
is a Jacobson category, and is indeed the universal Jacobson category associated to 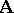 [a2].
[a2].
References
| [a1] | Y. Diers, "Jacobson categories" J. Algebra , 168 : 3 (1994) pp. 949–967 |
| [a2] | Y. Diers, "Clear objects in categories of commutative algebras" J. Pure Appl. Algebra , 10 (1995) pp. 155–171 |
Jacobson category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobson_category&oldid=12131