Jacobian
Jacobi determinant
A determinant of a matrix of special form whose entries are first-order partial derivatives of functions. Let 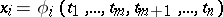 ,
, 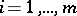 , be given functions having first-order partial derivatives with respect to the variables
, be given functions having first-order partial derivatives with respect to the variables 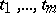 . The Jacobian of these functions is the determinant
. The Jacobian of these functions is the determinant
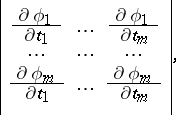 |
which for brevity is denoted by the symbol
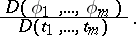 |
The modulus of a Jacobian characterizes the dilatation (contraction) of the volume element in the transition from the variables 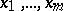 to
to 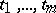 . The name is given after C.G.J. Jacobi, who first studied its properties and applications.
. The name is given after C.G.J. Jacobi, who first studied its properties and applications.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "Mathematical analysis" , 1–2 , Moscow (1973) (In Russian) |
| [3] | S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian) |
Comments
The above Jacobian is also denoted as
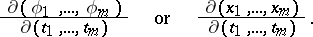 |
The entry at place 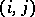 (
(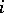 -th row,
-th row, 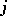 -th column) is
-th column) is  . The matrix with these entries is also called a Jacobian matrix (not to be confused with a Jacobi matrix). The Jacobian plays a role in the statement of the inverse function theorem and in change-of-variable formulas for integrals and differential forms.
. The matrix with these entries is also called a Jacobian matrix (not to be confused with a Jacobi matrix). The Jacobian plays a role in the statement of the inverse function theorem and in change-of-variable formulas for integrals and differential forms.
References
| [a1] | M. Spivak, "Calculus on manifolds" , Benjamin/Cummings (1965) |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
Jacobian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobian&oldid=14954