Jacobi symbol

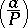A function defined for all integers coprime to a given odd integer 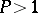as follows: Let 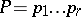be an expansion of 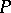into prime factors (not necessarily different), then

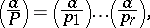where

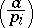is the Legendre symbol.

The Jacobi symbol is a generalization of the Legendre symbol and has similar properties. In particular, the reciprocity law:

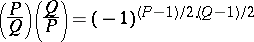holds, where 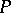and 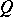are positive odd coprime numbers, and the supplementary formulas

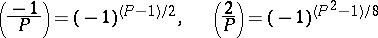are true.

The Jacobi symbol was introduced by C.G.J. Jacobi (1837).

References

[1]	C.G.J. Jacobi, "Gesammelte Werke" , 1–7 , Reimer (1881–1891)
[2]	P.G.L. Dirichlet, "Vorlesungen über Zahlentheorie" , Vieweg (1894)
[3]	P. Bachmann, "Niedere Zahlentheorie" , 1–2 , Teubner (1902–1910)

Comments

Considered as a function on 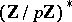, the Jacobi symbol is an example of a real character. This real character plays an important role in the decomposition of rational primes in a quadratic field (see [a1]).

References

[a1]	D.B. Zagier, "Zetafunktionen und quadratische Körper" , Springer (1981)