Isotropy group

The set of elements of a given group , acting on a set as a group of transformations, that leave a point fixed. This set turns out to be a subgroup of and is called the isotropy group of the point . The following terminology is used with the same meaning: stationary subgroup, stabilizer, -centralizer. If is a Hausdorff space and 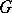is a topological group acting continuously on 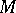, then 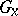is a closed subgroup. 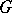If, furthermore, and are locally compact, has a countable base and acts transitively on 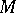, then there exists a unique homeomorphism from 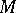into the quotient space 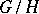, where is one of the isotropy groups; all the 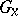, , are isomorphic to .

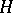Let 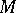be a smooth manifold and 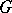a Lie group acting smoothly on 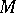. Then the isotropy group 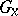of a point 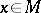induces a group of linear transformations of the tangent vector space 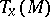; the latter is called the linear isotropy group at . On passing to tangent spaces of higher order at the point one obtains natural representations of the isotropy group in the structure groups of the corresponding tangent bundles of higher order; they are called the higher-order isotropy groups (see also Isotropy representation).

References

[1]	L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian)
[2]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)
[3]	R. Sulanke, P. Wintgen, "Differentialgeometrie und Faserbündel" , Deutsch. Verlag Wissenschaft. (1972)