Isotropic vector
A non-zero vector that is orthogonal to itself. Let  be a vector space over the field of real or complex numbers and let
be a vector space over the field of real or complex numbers and let  be a non-degenerate bilinear form of signature
be a non-degenerate bilinear form of signature  ,
,  ,
,  , on
, on 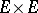 . Then an isotropic vector is a non-zero vector
. Then an isotropic vector is a non-zero vector  for which
for which  . One sometimes says that an isotropic vector has zero length (or norm). The set of all isotropic vectors is called the isotropic cone. A subspace
. One sometimes says that an isotropic vector has zero length (or norm). The set of all isotropic vectors is called the isotropic cone. A subspace  is called isotropic if there exists a non-zero vector
is called isotropic if there exists a non-zero vector 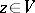 orthogonal to
orthogonal to 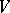 (that is, the restriction of
(that is, the restriction of 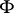 to
to 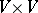 is degenerate:
is degenerate: 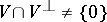 ). A vector subspace
). A vector subspace 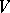 is said to be totally isotropic if all its vectors are isotropic vectors.
is said to be totally isotropic if all its vectors are isotropic vectors.
In the relativistic interpretation of the Universe, space-time is locally regarded as a four-dimensional vector space with a form of signature 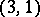 , the trajectories of photons are isotropic lines, while the isotropic cone is called the light cone.
, the trajectories of photons are isotropic lines, while the isotropic cone is called the light cone.
Isotropic vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isotropic_vector&oldid=18690