Isoperimetric inequality
(in geometry and physics)
A general term referring to the inequality  between the area
between the area  and perimeter
and perimeter  of a plane domain, to its various generalizations and to other inequalities between geometrical characteristics of figures, sets and manifolds. Also belonging to the general area of isoperimetric inequalities are estimates for quantities of physical origin (moments of inertia, torsional rigidity of an elastic beam, fundamental frequency of a membrane, electrostatic capacity, etc.) in terms of geometrical characteristics. An exact isoperimetric inequality is equivalent to the solution of some extremum problem. Isoperimetric inequalities can connect two or more quantities.
of a plane domain, to its various generalizations and to other inequalities between geometrical characteristics of figures, sets and manifolds. Also belonging to the general area of isoperimetric inequalities are estimates for quantities of physical origin (moments of inertia, torsional rigidity of an elastic beam, fundamental frequency of a membrane, electrostatic capacity, etc.) in terms of geometrical characteristics. An exact isoperimetric inequality is equivalent to the solution of some extremum problem. Isoperimetric inequalities can connect two or more quantities.
For the best known isoperimetric inequalities, namely the classical one and its analogues in the Minkowski spaces  , the Lobachevskii spaces
, the Lobachevskii spaces  , the spheres
, the spheres  , as well as for refinements of them, see Isoperimetric inequality, classical.
, as well as for refinements of them, see Isoperimetric inequality, classical.
An extensive coverage of isoperimetric inequalities between the elements of the simplest figures, mainly polygons, can be found in [1]. Such isoperimetric inequalities are called geometric inequalities.
For elementary isoperimetric inequalities between such parameters of sets in  as the volume
as the volume  , the diameter
, the diameter  and the radius
and the radius 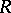 of the smallest circumscribed ball, etc., see [2] and [3]. Among them are: Young's inequality:
of the smallest circumscribed ball, etc., see [2] and [3]. Among them are: Young's inequality:
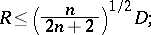 |
Gale's inequality:
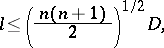 |
where 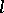 is the length of the edge of the smallest circumscribed regular simplex; Bieberbach's inequality:
is the length of the edge of the smallest circumscribed regular simplex; Bieberbach's inequality:
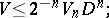 |
and the Loomis–Whitney inequality:
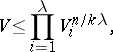 |
where 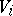 is the
is the 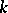 -dimensional volume of the projection of the set onto the
-dimensional volume of the projection of the set onto the  -th of the
-th of the 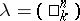 pairwise-different
pairwise-different 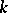 -dimensional Cartesian coordinate planes. The first three inequalities can be generalized to the spaces
-dimensional Cartesian coordinate planes. The first three inequalities can be generalized to the spaces 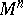 ,
, 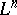 ,
, 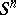 (see [4], [5]). In Bieberbach's inequality, the diameter can be replaced by the mean width (see [5]).
(see [4], [5]). In Bieberbach's inequality, the diameter can be replaced by the mean width (see [5]).
In connection with problems of arrangement and covering, isoperimetric inequalities are considered that are specific for polyhedra, with the introduction of the number of edges or the sum of their lengths, etc. (see [6]).
For convex bodies, many isoperimetric inequalities (including the classical ones and a number of inequalities between integrals of symmetric functions of principal curvatures) are special cases of inequalities between composite objects (see Mixed-volume theory; Minkowski inequality).
The use of isoperimetric inequalities as estimates for some parameters of figures in terms of others arose within the limits of geometry. The class of isoperimetric inequalities is enriched by mathematical physics, the theory of functions of a complex variable, functional analysis, the theory of approximations of functions, and the calculus of variations. Isoperimetric inequalities in Riemannian geometry are noticeably more complex.
In mathematical physics, isoperimetric inequalities arose (firstly as conjectures) in papers of A. Saint-Venant (1856):
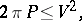 |
where 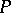 is the torsional rigidity of a prismatic elastic beam; of Lord Rayleigh (1877):
is the torsional rigidity of a prismatic elastic beam; of Lord Rayleigh (1877):
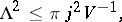 |
where 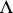 is the fundamental frequency of the membrane and
is the fundamental frequency of the membrane and 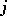 is the first positive root of the Bessel function
is the first positive root of the Bessel function 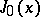 ; and in papers of H. Poincaré (1903):
; and in papers of H. Poincaré (1903):
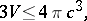 |
where  is the electrostatic capacity of the body. In these inequalities,
is the electrostatic capacity of the body. In these inequalities, 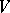 is, respectively, the cross-sectional area of the beam, the area of the membrane and the volume of the body. Numerous results of this sort are summarized in [7] and [8]. Certain estimates for the first eigen value
is, respectively, the cross-sectional area of the beam, the area of the membrane and the volume of the body. Numerous results of this sort are summarized in [7] and [8]. Certain estimates for the first eigen value 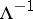 of the Laplace operator on closed Riemannian manifolds can be found in [9].
of the Laplace operator on closed Riemannian manifolds can be found in [9].
In functional analysis, conditions for boundedness and compactness of imbedding operators (see Imbedding theorems) for Sobolev spaces have been given in terms of isoperimetric inequalities (connecting measure and capacity) (see [10], [11]).
For example, the estimate
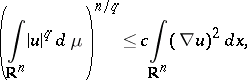 |
where 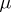 is a non-negative measure,
is a non-negative measure, 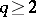 ,
,  , is valid for all
, is valid for all 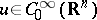 if and only if the following isoperimetric inequality is satisfied for all compacta
if and only if the following isoperimetric inequality is satisfied for all compacta 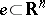 :
:
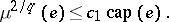 |
Here 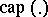 is the Wiener capacity (see Capacity).
is the Wiener capacity (see Capacity).
Isoperimetric inequalities for volume and area are used in the proof of a priori estimates for solutions of linear and quasi-linear elliptic equations (see [12], [26]).
Specific isoperimetric inequalities arise for convex bodies in a Minkowski space in connection with the theory of approximation of functions (see Self-perimeter; Width).
Applying isoperimetric inequalities is a standard device in the theory of conformal and quasi-conformal mappings. Inequality (4) below is an example of a conformally-invariant isoperimetric inequality.
Isoperimetric inequalities involving the mean curvature of a submanifold, in particular for minimal surfaces, play an important part in the solution of the Plateau problem.
In the Riemannian geometry of non-homogeneous spaces, generalizations of the classical isoperimetric inequalities have been studied in detail only in the two-dimensional case. Let 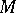 be a simply-connected compact two-dimensional manifold with boundary such that the positive part
be a simply-connected compact two-dimensional manifold with boundary such that the positive part 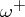 of the integral curvature of
of the integral curvature of 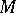 is less than
is less than 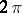 . Then (see [13]):
. Then (see [13]):
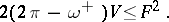 | (1) |
The isoperimetric inequality (1) is valid also for a two-dimensional manifold of bounded curvature, which is a more general type of manifold than a Riemannian manifold. Equality in (1) is attained for a non-regular object — a domain isometric to the lateral surface of a right circular cone with complete angle 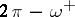 about the vertex. Using (1), inequalities can be established for the length of a curve, inside the domain, in dependence on
about the vertex. Using (1), inequalities can be established for the length of a curve, inside the domain, in dependence on 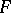 ,
, 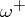 and the proper rotation (cf. Winding number). In particular, for the geodesic length
and the proper rotation (cf. Winding number). In particular, for the geodesic length 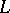 ,
,
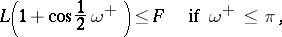 |
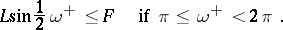 |
Isoperimetric inequality (1) is a special case of the estimate
 | (2) |
where  is any real number,
is any real number, 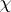 is the Euler characteristic of the compact domain with boundary,
is the Euler characteristic of the compact domain with boundary, 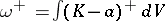 , and
, and 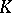 is the Gaussian curvature. Similar to (2) are estimates for the area of a
is the Gaussian curvature. Similar to (2) are estimates for the area of a 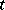 -neighbourhood of the boundary of a domain and for the largest distance of points in the domain from the boundary (see [14]). If the surface
-neighbourhood of the boundary of a domain and for the largest distance of points in the domain from the boundary (see [14]). If the surface 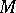 is a smooth submanifold in
is a smooth submanifold in 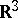 , then the estimates (1), (2) are supplemented by isoperimetric inequalities involving the external characteristics of the surface. For closed surfaces, the following sharp isoperimetric inequality follows from integral identities (see [15]):
, then the estimates (1), (2) are supplemented by isoperimetric inequalities involving the external characteristics of the surface. For closed surfaces, the following sharp isoperimetric inequality follows from integral identities (see [15]):
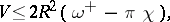 |
where 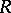 is the radius of a ball in
is the radius of a ball in 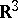 containing
containing  . Similar (but non-sharp) inequalities have been obtained also for surfaces with boundary (see [16]). In particular, for a simply-connected saddle surface in
. Similar (but non-sharp) inequalities have been obtained also for surfaces with boundary (see [16]). In particular, for a simply-connected saddle surface in 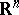 with boundary length
with boundary length 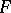 :
:
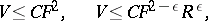 |
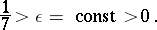 |
The inequalities mentioned remain true for general (non-regular) surfaces in  ,
, 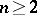 , if instead of
, if instead of 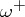 the positive exterior curvature is taken into consideration — a measure in the set of locally supporting planes (see [16]).
the positive exterior curvature is taken into consideration — a measure in the set of locally supporting planes (see [16]).
For an  -dimensional Riemannian space
-dimensional Riemannian space 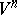 , isoperimetric inequalities are usually connected with one-sided bounds on the sectional curvature or the Ricci curvature. The simplest is a bound for the volume
, isoperimetric inequalities are usually connected with one-sided bounds on the sectional curvature or the Ricci curvature. The simplest is a bound for the volume 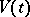 of the ball of radius
of the ball of radius 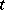 in
in 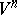 in terms of the volume
in terms of the volume  of a ball of the same radius in a complete simply-connected surface of constant curvature
of a ball of the same radius in a complete simply-connected surface of constant curvature 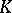 :
:
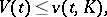 | (3) |
where 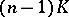 is the smallest value of the Ricci curvature in
is the smallest value of the Ricci curvature in 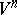 ; if
; if 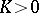 , then it is assumed that
, then it is assumed that  (see [17]). Similar isoperimetric inequalities are valid for a tubular
(see [17]). Similar isoperimetric inequalities are valid for a tubular 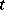 -neighbourhood of a
-neighbourhood of a 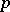 -dimensional submanifold of
-dimensional submanifold of 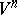 ,
, 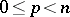 ; the minimum of the sectional curvatures in
; the minimum of the sectional curvatures in 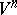 and the maximum of the normal curvatures of submanifolds participate in such an isoperimetric inequality (instead of the Ricci curvature) (see [18]).
and the maximum of the normal curvatures of submanifolds participate in such an isoperimetric inequality (instead of the Ricci curvature) (see [18]).
If the least upper bound  of the sectional curvatures is negative, then the volume
of the sectional curvatures is negative, then the volume 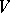 of the closed manifold is bounded from below by
of the closed manifold is bounded from below by 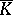 (see [19]). The following linear isoperimetric inequality holds for a domain
(see [19]). The following linear isoperimetric inequality holds for a domain 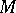 in a complete simply-connected
in a complete simply-connected 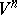 :
:
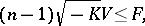 |
where 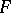 is the
is the  -dimensional area of the boundary of
-dimensional area of the boundary of 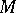 , and also the isoperimetric inequality
, and also the isoperimetric inequality
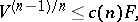 |
the exact value of 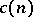 being unknown.
being unknown.
In spaces of negative curvature, a number of estimates have been obtained for convex domains that generalize isoperimetric inequalities for convex bodies in 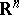 (see [20], [21]). Thus,
(see [20], [21]). Thus,
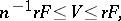 |
where  is the greatest distance of points of
is the greatest distance of points of 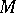 from the boundary. If the greatest lower bound
from the boundary. If the greatest lower bound 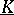 of the sectional curvatures in
of the sectional curvatures in 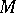 is positive, then
is positive, then 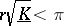 , and the left inequality can be sharpened:
, and the left inequality can be sharpened:
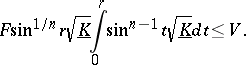 |
The inequality 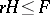 holds, where
holds, where 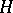 is the integral mean curvature. The following isoperimetric inequality holds in the three-dimensional case:
is the integral mean curvature. The following isoperimetric inequality holds in the three-dimensional case:
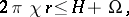 |
where 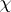 is the Euler characteristic of the boundary of
is the Euler characteristic of the boundary of 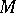 and
and  is the integral scalar curvature of
is the integral scalar curvature of 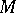 .
.
In the classical isoperimetric inequality, the area is bounded from above. For closed simply-connected surfaces, the area can be bounded from below in terms of the length 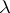 of the shortest loop that is not homotopic to zero:
of the shortest loop that is not homotopic to zero:
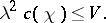 | (4) |
The exact value of 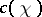 is known only for the torus
is known only for the torus 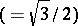 and the projective plane
and the projective plane 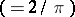 . Inequality (4) is a corollary of the following isoperimetric inequality (see [22]):
. Inequality (4) is a corollary of the following isoperimetric inequality (see [22]):
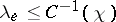 | (4prm) |
for the extremal length 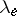 of the family of loops that are not homotopic to zero.
of the family of loops that are not homotopic to zero.
The problem of similar inequalities for 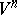 with
with 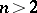 is discussed in [22]. If
is discussed in [22]. If 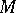 is a topological
is a topological  -dimensional cube with interior metric
-dimensional cube with interior metric 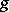 , then its
, then its  -volume satisfies the inequality
-volume satisfies the inequality
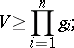 |
here 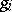 is the distance in the metric
is the distance in the metric 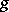 between the
between the 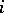 -th pair of opposite
-th pair of opposite 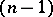 -dimensional faces. See [24], [25] for more details.
-dimensional faces. See [24], [25] for more details.
In the theory of minimal surfaces and surfaces like them, a number of isoperimetric inequalities have been obtained that hold not only for smooth 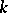 -dimensional submanifolds in
-dimensional submanifolds in 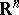 ,
, 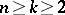 , but also for more general
, but also for more general 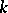 -dimensional "films" : submanifolds with singularities, currents, etc. Thus, the following inequality was established in [26], [27]:
-dimensional "films" : submanifolds with singularities, currents, etc. Thus, the following inequality was established in [26], [27]:
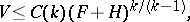 | (5) |
where 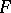 is the
is the  -area of a face and
-area of a face and 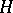 is the integral of the modulus of the mean curvature
is the integral of the modulus of the mean curvature 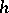 of the film. If
of the film. If 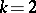 , then the following isoperimetric inequality holds when
, then the following isoperimetric inequality holds when 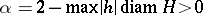 :
:
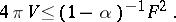 |
In methods of proof and applications, lower bounds for the volume 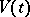 of the intersection of a
of the intersection of a 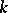 -film
-film 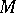 with the ball of radius
with the ball of radius 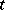 and centre at
and centre at 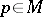 belong to the class of inequalities of the type (5). Thus, for a minimal surface
belong to the class of inequalities of the type (5). Thus, for a minimal surface 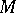 the function
the function 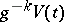 increases for all
increases for all 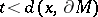 . See [27], [28] for some generalizations to minimal films in
. See [27], [28] for some generalizations to minimal films in 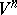 (and to films under the assumption that
(and to films under the assumption that 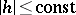 ).
).
References
| [1] | O. Bottema, "Geometric inequalities" , Noordhoff (1969) |
| [2] | H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) |
| [3] | T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934) |
| [4] | L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 101–180 |
| [5] | M.S. Mel'nikov, "On the relation between volume and diameter of sets in  -dimensional Banach space" Uspekhi Mat. Nauk , 18 : 4 (1963) pp. 165–170 (In Russian) -dimensional Banach space" Uspekhi Mat. Nauk , 18 : 4 (1963) pp. 165–170 (In Russian) |
| [6] | L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) |
| [7] | G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951) |
| [8] | L.E. Payne, "Isoperimetric inequalities and their applications" Siam Rev. , 9 : 3 (1967) pp. 453–488 |
| [9] | M. Berger, P. Ganduchon, E. Mazet, "Le spectre d'une variété riemannienne" , Springer (1971) |
| [10] | V.G. Maz'ya, "Certain integral inequalities for functions of several variables" , Problems in mathematical analysis , 3 , Leningrad (1972) pp. 33–68 (In Russian) |
| [11] | V.G. Maz'ya, "Classes of sets and measures connected with imbedding theorems" , Imbedding theorems and their applications , Moscow (1970) pp. 142–159 (In Russian) |
| [12] | V.G. Maz'ya, "On weak solutions of the Dirichlet and Neumann problems" Trans. Moscow Math. Soc. , 20 (1969) pp. 135–172 Trudy Moskov. Mat. Obshch. , 20 (1969) pp. 137–172 |
| [13] | A.D. Aleksandrov, V.V. Strel'tsov, "Isoperimetric problem and estimates of the length of a curve on a surface" Proc. Steklov Inst. Math. , 76 (1965) pp. 81–99 Trudy Mat. Inst. Steklov. , 76 (1965) pp. 67–80 |
| [14] | Yu.D. Burago, "Note on the isoperimetric inequality on two-dimensional surfaces" Siberian Math. J. , 14 : 3 (1973) pp. 463–465 Sibirsk. Mat. Zh. , 14 : 3 (1973) pp. 666–668 |
| [15] | J.K. Shahin, "Some integral formulas for closed hypersurfaces in Euclidean space" Proc. Amer. Math. Soc. , 19 : 3 (1968) pp. 609–613 |
| [16] | Yu.D. Burago, "Isoperimetric inequalities in the theory of surfaces of bounded external curvature" , Consultants Bureau (1970) (Translated from Russian) |
| [17] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) |
| [18] | J. Cheeger, "Finiteness theorems for Riemannian manifolds" Amer. J. Math. , 92 : 1 (1970) pp. 61–74 |
| [19] | G.A. Margulis, "Thesis" , VI All-Union Topological Conference , Tbilisi (1972) (In Russian) |
| [20] | B.V. Dekster, "Estimates of the volume of a region in a Riemannian space" Math. USSR Sb. , 17 : 1 (1972) pp. 61–87 Mat. Sb. , 88 : 1 (1972) pp. 61–87 |
| [21] | Yu.A. Volkov, B.V. Dekster, "Estimates of the curvature of a three-dimensional evolute" Math. USSR Sb. , 12 : 4 (1970) pp. 615–640 Mat. Sb. , 83 : 4 (1970) pp. 616–638 |
| [22] | M. Berger, "Du côté de chez Pu" Ann. Sci. École Norm Sup. Sér. 4 , 5 : 1 (1972) pp. 1–44 |
| [23] | M. Berger, "A l'ombre de Loewner" Ann. Sci. École Norm. Sup. Sér. 4 , 5 : 2 (1972) pp. 241–260 |
| [24] | W.R. Derrick, "A weighted volume-diameter inequality for  -cubes" J. Math. Mech. , 18 : 5 (1968) pp. 453–472 -cubes" J. Math. Mech. , 18 : 5 (1968) pp. 453–472 |
| [25] | F. Almgren, "An isoperimetric inequality" Proc. Amer. Math. Soc. , 15 : 2 (1964) pp. 284–285 |
| [26] | J. Michael, L. Simon, "Sobolev and mean-value inequalities on generalized submanifolds of 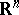 " Comm. Pure Appl. Math. , 26 : 23 (1973) pp. 361–379 " Comm. Pure Appl. Math. , 26 : 23 (1973) pp. 361–379 |
| [27] | W. Allard, "On the first variation of a varifold" Ann. of Math. , 95 (1972) pp. 417–491 |
| [28] | A.T. Fomenko, "Minimal compacta in Riemannian manifolds and a conjecture of Reifenberg" Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 5 (1972) pp. 1049–1079 (In Russian) |
Comments
For an up-to-date account of geometric inequalities supplementing [1], see [a3].
References
| [a1] | C. Bandle, "Isoperimetric inequalities and applications" , Pitman (1980) |
| [a2] | H. Kaul, "Isoperimetrische Ungleichung und Gauss–Bonnet–Formel für 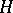 -Flächen in Riemannsche Mannigfaltigkeiten" Arch. Rat. Mech. Anal. , 45 (1972) pp. 194–221 -Flächen in Riemannsche Mannigfaltigkeiten" Arch. Rat. Mech. Anal. , 45 (1972) pp. 194–221 |
| [a3] | D.S. Mitrinović, J.E. Pečarić, V. Volenec, "Recent advances in geometric inequalities" , Kluwer (1989) |
Isoperimetric inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isoperimetric_inequality&oldid=13532