Difference between revisions of "Isoperimetric inequality"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | i0528601.png | ||
| + | $#A+1 = 154 n = 4 | ||
| + | $#C+1 = 154 : ~/encyclopedia/old_files/data/I052/I.0502860 Isoperimetric inequality | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''(in geometry and physics)'' | ''(in geometry and physics)'' | ||
| − | A general term referring to the inequality | + | A general term referring to the inequality $ 4 \pi V \leq F ^ { 2 } $ |
| + | between the area $ V $ | ||
| + | and perimeter $ F $ | ||
| + | of a plane domain, to its various generalizations and to other inequalities between geometrical characteristics of figures, sets and manifolds. Also belonging to the general area of isoperimetric inequalities are estimates for quantities of physical origin (moments of inertia, torsional rigidity of an elastic beam, fundamental frequency of a membrane, electrostatic capacity, etc.) in terms of geometrical characteristics. An exact isoperimetric inequality is equivalent to the solution of some extremum problem. Isoperimetric inequalities can connect two or more quantities. | ||
| − | For the best known isoperimetric inequalities, namely the classical one and its analogues in the Minkowski spaces | + | For the best known isoperimetric inequalities, namely the classical one and its analogues in the Minkowski spaces $ M ^ {n} $, |
| + | the Lobachevskii spaces $ L ^ {n} $, | ||
| + | the spheres $ S ^ {n} $, | ||
| + | as well as for refinements of them, see [[Isoperimetric inequality, classical|Isoperimetric inequality, classical]]. | ||
An extensive coverage of isoperimetric inequalities between the elements of the simplest figures, mainly polygons, can be found in [[#References|[1]]]. Such isoperimetric inequalities are called geometric inequalities. | An extensive coverage of isoperimetric inequalities between the elements of the simplest figures, mainly polygons, can be found in [[#References|[1]]]. Such isoperimetric inequalities are called geometric inequalities. | ||
| − | For elementary isoperimetric inequalities between such parameters of sets in | + | For elementary isoperimetric inequalities between such parameters of sets in $ \mathbf R ^ {n} $ |
| + | as the volume $ V $, | ||
| + | the diameter $ D $ | ||
| + | and the radius $ R $ | ||
| + | of the smallest circumscribed ball, etc., see [[#References|[2]]] and [[#References|[3]]]. Among them are: Young's inequality: | ||
| − | + | $$ | |
| + | R \leq \left ( { | ||
| + | \frac{n}{2n + 2 } | ||
| + | } \right ) ^ {1/2} D; | ||
| + | $$ | ||
Gale's inequality: | Gale's inequality: | ||
| − | + | $$ | |
| + | l \leq \left ( { | ||
| + | \frac{n ( n + 1) }{2} | ||
| + | } \right ) ^ {1/2} D, | ||
| + | $$ | ||
| − | where | + | where $ l $ |
| + | is the length of the edge of the smallest circumscribed regular simplex; Bieberbach's inequality: | ||
| − | + | $$ | |
| + | V \leq 2 ^ {-} n V _ {n} D ^ {n} ; | ||
| + | $$ | ||
and the Loomis–Whitney inequality: | and the Loomis–Whitney inequality: | ||
| − | + | $$ | |
| + | V \leq \ | ||
| + | \prod _ {i = 1 } ^ \lambda V _ {i} ^ {n/k \lambda } , | ||
| + | $$ | ||
| − | where | + | where $ V _ {i} $ |
| + | is the $ k $- | ||
| + | dimensional volume of the projection of the set onto the $ i $- | ||
| + | th of the $ \lambda = ( {} _ {k} ^ {n} ) $ | ||
| + | pairwise-different $ k $- | ||
| + | dimensional Cartesian coordinate planes. The first three inequalities can be generalized to the spaces $ M ^ {n} $, | ||
| + | $ L ^ {n} $, | ||
| + | $ S ^ {n} $( | ||
| + | see [[#References|[4]]], [[#References|[5]]]). In Bieberbach's inequality, the diameter can be replaced by the mean width (see [[#References|[5]]]). | ||
In connection with problems of [[Arrangement|arrangement]] and [[Covering|covering]], isoperimetric inequalities are considered that are specific for polyhedra, with the introduction of the number of edges or the sum of their lengths, etc. (see [[#References|[6]]]). | In connection with problems of [[Arrangement|arrangement]] and [[Covering|covering]], isoperimetric inequalities are considered that are specific for polyhedra, with the introduction of the number of edges or the sum of their lengths, etc. (see [[#References|[6]]]). | ||
| Line 33: | Line 77: | ||
In mathematical physics, isoperimetric inequalities arose (firstly as conjectures) in papers of A. Saint-Venant (1856): | In mathematical physics, isoperimetric inequalities arose (firstly as conjectures) in papers of A. Saint-Venant (1856): | ||
| − | + | $$ | |
| + | 2 \pi P \leq V ^ {2} , | ||
| + | $$ | ||
| − | where | + | where $ P $ |
| + | is the torsional rigidity of a prismatic elastic beam; of Lord Rayleigh (1877): | ||
| − | + | $$ | |
| + | \Lambda ^ {2} \leq \pi j ^ {2} V ^ {-} 1 , | ||
| + | $$ | ||
| − | where | + | where $ \Lambda $ |
| + | is the fundamental frequency of the membrane and $ j $ | ||
| + | is the first positive root of the Bessel function $ J _ {0} ( x) $; | ||
| + | and in papers of H. Poincaré (1903): | ||
| − | + | $$ | |
| + | 3V \leq 4 \pi c ^ {3} , | ||
| + | $$ | ||
| − | where | + | where $ c $ |
| + | is the electrostatic capacity of the body. In these inequalities, $ V $ | ||
| + | is, respectively, the cross-sectional area of the beam, the area of the membrane and the volume of the body. Numerous results of this sort are summarized in [[#References|[7]]] and [[#References|[8]]]. Certain estimates for the first eigen value $ \Lambda ^ {-} 1 $ | ||
| + | of the Laplace operator on closed Riemannian manifolds can be found in [[#References|[9]]]. | ||
In functional analysis, conditions for boundedness and compactness of imbedding operators (see [[Imbedding theorems|Imbedding theorems]]) for Sobolev spaces have been given in terms of isoperimetric inequalities (connecting measure and capacity) (see [[#References|[10]]], [[#References|[11]]]). | In functional analysis, conditions for boundedness and compactness of imbedding operators (see [[Imbedding theorems|Imbedding theorems]]) for Sobolev spaces have been given in terms of isoperimetric inequalities (connecting measure and capacity) (see [[#References|[10]]], [[#References|[11]]]). | ||
| Line 49: | Line 106: | ||
For example, the estimate | For example, the estimate | ||
| − | + | $$ | |
| + | \left ( \int\limits _ {\mathbf R ^ {n} } | u | ^ {q} d \mu | ||
| + | \right ) ^ {n/q} \leq \ | ||
| + | c \int\limits _ {\mathbf R ^ {n} } ( \nabla u) ^ {2} dx, | ||
| + | $$ | ||
| − | where | + | where $ \mu $ |
| + | is a non-negative measure, $ q \geq 2 $, | ||
| + | $ n > 2 $, | ||
| + | is valid for all $ u \in C _ {0} ^ \infty ( \mathbf R ^ {n} ) $ | ||
| + | if and only if the following isoperimetric inequality is satisfied for all compacta $ e \subset \mathbf R ^ {n} $: | ||
| − | + | $$ | |
| + | \mu ^ {2/q} ( e) \leq c _ {1} \mathop{\rm cap} ( e). | ||
| + | $$ | ||
| − | Here | + | Here $ \mathop{\rm cap} ( \cdot ) $ |
| + | is the Wiener capacity (see [[Capacity|Capacity]]). | ||
Isoperimetric inequalities for volume and area are used in the proof of a priori estimates for solutions of linear and quasi-linear elliptic equations (see [[#References|[12]]], [[#References|[26]]]). | Isoperimetric inequalities for volume and area are used in the proof of a priori estimates for solutions of linear and quasi-linear elliptic equations (see [[#References|[12]]], [[#References|[26]]]). | ||
| Line 65: | Line 133: | ||
Isoperimetric inequalities involving the mean curvature of a submanifold, in particular for minimal surfaces, play an important part in the solution of the [[Plateau problem|Plateau problem]]. | Isoperimetric inequalities involving the mean curvature of a submanifold, in particular for minimal surfaces, play an important part in the solution of the [[Plateau problem|Plateau problem]]. | ||
| − | In the Riemannian geometry of non-homogeneous spaces, generalizations of the classical isoperimetric inequalities have been studied in detail only in the two-dimensional case. Let | + | In the Riemannian geometry of non-homogeneous spaces, generalizations of the classical isoperimetric inequalities have been studied in detail only in the two-dimensional case. Let $ M $ |
| + | be a simply-connected compact two-dimensional manifold with boundary such that the positive part $ \omega ^ {+} $ | ||
| + | of the integral curvature of $ M $ | ||
| + | is less than $ 2 \pi $. | ||
| + | Then (see [[#References|[13]]]): | ||
| − | + | $$ \tag{1 } | |
| + | 2 ( 2 \pi - \omega ^ {+} ) V \leq F ^ { 2 } . | ||
| + | $$ | ||
| − | The isoperimetric inequality (1) is valid also for a [[Two-dimensional manifold of bounded curvature|two-dimensional manifold of bounded curvature]], which is a more general type of manifold than a Riemannian manifold. Equality in (1) is attained for a non-regular object — a domain isometric to the lateral surface of a right circular cone with complete angle | + | The isoperimetric inequality (1) is valid also for a [[Two-dimensional manifold of bounded curvature|two-dimensional manifold of bounded curvature]], which is a more general type of manifold than a Riemannian manifold. Equality in (1) is attained for a non-regular object — a domain isometric to the lateral surface of a right circular cone with complete angle $ 2 \pi - \omega ^ {+} $ |
| + | about the vertex. Using (1), inequalities can be established for the length of a curve, inside the domain, in dependence on $ F $, | ||
| + | $ \omega ^ {+} $ | ||
| + | and the proper rotation (cf. [[Winding number|Winding number]]). In particular, for the geodesic length $ L $, | ||
| − | + | $$ | |
| + | L \left ( 1 + \cos { | ||
| + | \frac{1}{2} | ||
| + | } \omega ^ {+} \right ) \leq F \ \ | ||
| + | \textrm{ if } \omega ^ {+} \leq \pi , | ||
| + | $$ | ||
| − | < | + | $$ |
| + | L \sin { | ||
| + | \frac{1}{2} | ||
| + | } \omega ^ {+} \leq F \ \textrm{ if } \pi \leq \omega ^ {+} < 2 \pi . | ||
| + | $$ | ||
Isoperimetric inequality (1) is a special case of the estimate | Isoperimetric inequality (1) is a special case of the estimate | ||
| − | + | $$ \tag{2 } | |
| + | F ^ { 2 } + 2 | ||
| + | ( \omega _ {a} ^ {+} - 2 \pi \chi ) V + aV \geq 0, | ||
| + | $$ | ||
| − | where | + | where $ a $ |
| + | is any real number, $ \chi $ | ||
| + | is the [[Euler characteristic|Euler characteristic]] of the compact domain with boundary, $ \omega ^ {+} = \int ( K - a) ^ {+} dV $, | ||
| + | and $ K $ | ||
| + | is the [[Gaussian curvature|Gaussian curvature]]. Similar to (2) are estimates for the area of a $ t $- | ||
| + | neighbourhood of the boundary of a domain and for the largest distance of points in the domain from the boundary (see [[#References|[14]]]). If the surface $ M $ | ||
| + | is a smooth submanifold in $ \mathbf R ^ {3} $, | ||
| + | then the estimates (1), (2) are supplemented by isoperimetric inequalities involving the external characteristics of the surface. For closed surfaces, the following sharp isoperimetric inequality follows from integral identities (see [[#References|[15]]]): | ||
| − | + | $$ | |
| + | V \leq 2R ^ {2} ( \omega ^ {+} - \pi \chi ), | ||
| + | $$ | ||
| − | where | + | where $ R $ |
| + | is the radius of a ball in $ \mathbf R ^ {3} $ | ||
| + | containing $ M $. | ||
| + | Similar (but non-sharp) inequalities have been obtained also for surfaces with boundary (see [[#References|[16]]]). In particular, for a simply-connected saddle surface in $ \mathbf R ^ {n} $ | ||
| + | with boundary length $ F $: | ||
| − | + | $$ | |
| + | V \leq CF ^ { 2 } ,\ \ | ||
| + | V \leq CF ^ { 2 - \epsilon } R ^ \epsilon , | ||
| + | $$ | ||
| − | + | $$ | |
| + | { | ||
| + | \frac{1}{7} | ||
| + | } > \epsilon = \textrm{ const } > 0. | ||
| + | $$ | ||
| − | The inequalities mentioned remain true for general (non-regular) surfaces in | + | The inequalities mentioned remain true for general (non-regular) surfaces in $ \mathbf R ^ {n} $, |
| + | $ n \geq 2 $, | ||
| + | if instead of $ \omega ^ {+} $ | ||
| + | the positive exterior curvature is taken into consideration — a measure in the set of locally supporting planes (see [[#References|[16]]]). | ||
| − | For an | + | For an $ n $- |
| + | dimensional Riemannian space $ V ^ {n} $, | ||
| + | isoperimetric inequalities are usually connected with one-sided bounds on the [[Sectional curvature|sectional curvature]] or the [[Ricci curvature|Ricci curvature]]. The simplest is a bound for the volume $ V ( t) $ | ||
| + | of the ball of radius $ t $ | ||
| + | in $ V ^ {n} $ | ||
| + | in terms of the volume $ v ( t, K) $ | ||
| + | of a ball of the same radius in a complete simply-connected surface of constant curvature $ K $: | ||
| − | + | $$ \tag{3 } | |
| + | V ( t) \leq v ( t, K), | ||
| + | $$ | ||
| − | where | + | where $ ( n - 1) K $ |
| + | is the smallest value of the Ricci curvature in $ V ^ {n} $; | ||
| + | if $ K > 0 $, | ||
| + | then it is assumed that $ t \leq \pi / \sqrt K $( | ||
| + | see [[#References|[17]]]). Similar isoperimetric inequalities are valid for a tubular $ t $- | ||
| + | neighbourhood of a $ p $- | ||
| + | dimensional submanifold of $ V ^ {n} $, | ||
| + | $ 0 \leq p < n $; | ||
| + | the minimum of the sectional curvatures in $ V ^ {n} $ | ||
| + | and the maximum of the normal curvatures of submanifolds participate in such an isoperimetric inequality (instead of the Ricci curvature) (see [[#References|[18]]]). | ||
| − | If the least upper bound | + | If the least upper bound $ \overline{K}\; $ |
| + | of the sectional curvatures is negative, then the volume $ V $ | ||
| + | of the closed manifold is bounded from below by $ \overline{K}\; $( | ||
| + | see [[#References|[19]]]). The following linear isoperimetric inequality holds for a domain $ M $ | ||
| + | in a complete simply-connected $ V ^ {n} $: | ||
| − | + | $$ | |
| + | ( n - 1) \sqrt {- K } V \leq F, | ||
| + | $$ | ||
| − | where | + | where $ F $ |
| + | is the $ ( n - 1) $- | ||
| + | dimensional area of the boundary of $ M $, | ||
| + | and also the isoperimetric inequality | ||
| − | + | $$ | |
| + | V ^ {( n - 1)/n } \leq c ( n) F, | ||
| + | $$ | ||
| − | the exact value of | + | the exact value of $ c ( n) $ |
| + | being unknown. | ||
| − | In spaces of negative curvature, a number of estimates have been obtained for convex domains that generalize isoperimetric inequalities for convex bodies in | + | In spaces of negative curvature, a number of estimates have been obtained for convex domains that generalize isoperimetric inequalities for convex bodies in $ \mathbf R ^ {n} $( |
| + | see [[#References|[20]]], [[#References|[21]]]). Thus, | ||
| − | + | $$ | |
| + | n ^ {-} 1 rF \leq V \leq rF, | ||
| + | $$ | ||
| − | where | + | where $ r $ |
| + | is the greatest distance of points of $ M $ | ||
| + | from the boundary. If the greatest lower bound $ \underline{K} $ | ||
| + | of the sectional curvatures in $ M $ | ||
| + | is positive, then $ r \sqrt {\underline{K} } < \pi $, | ||
| + | and the left inequality can be sharpened: | ||
| − | + | $$ | |
| + | F \sin ^ {1/n} r \sqrt {\underline{K} } | ||
| + | \int\limits _ { 0 } ^ { r } \sin ^ {n - 1 } t \sqrt {\underline{K} } \ | ||
| + | dt \leq V. | ||
| + | $$ | ||
| − | The inequality | + | The inequality $ rH \leq F $ |
| + | holds, where $ H $ | ||
| + | is the integral [[Mean curvature|mean curvature]]. The following isoperimetric inequality holds in the three-dimensional case: | ||
| − | + | $$ | |
| + | 2 \pi \chi r \leq H + \Omega , | ||
| + | $$ | ||
| − | where | + | where $ \chi $ |
| + | is the Euler characteristic of the boundary of $ M $ | ||
| + | and $ \Omega $ | ||
| + | is the integral [[Scalar curvature|scalar curvature]] of $ M $. | ||
| − | In the classical isoperimetric inequality, the area is bounded from above. For closed simply-connected surfaces, the area can be bounded from below in terms of the length | + | In the classical isoperimetric inequality, the area is bounded from above. For closed simply-connected surfaces, the area can be bounded from below in terms of the length $ \lambda $ |
| + | of the shortest loop that is not homotopic to zero: | ||
| − | + | $$ \tag{4 } | |
| + | \lambda ^ {2} | ||
| + | c ( \chi ) \leq V. | ||
| + | $$ | ||
| − | The exact value of | + | The exact value of $ c ( \chi ) $ |
| + | is known only for the torus $ ( = \sqrt 3 /2) $ | ||
| + | and the projective plane $ ( = 2/ \pi ) $. | ||
| + | Inequality (4) is a corollary of the following isoperimetric inequality (see [[#References|[22]]]): | ||
| − | + | $$ \tag{4'} | |
| + | \lambda _ {e} \leq C ^ {-} 1 ( \chi ) | ||
| + | $$ | ||
| − | for the extremal length | + | for the extremal length $ \lambda _ {e} $ |
| + | of the family of loops that are not homotopic to zero. | ||
| − | The problem of similar inequalities for | + | The problem of similar inequalities for $ V ^ {n} $ |
| + | with $ n > 2 $ | ||
| + | is discussed in [[#References|[22]]]. If $ M $ | ||
| + | is a topological $ n $- | ||
| + | dimensional cube with interior metric $ g $, | ||
| + | then its $ n $- | ||
| + | volume satisfies the inequality | ||
| − | + | $$ | |
| + | V \geq \prod _ {i = 1 } ^ { n } g _ {i} ; | ||
| + | $$ | ||
| − | here | + | here $ g _ {i} $ |
| + | is the distance in the metric $ g $ | ||
| + | between the $ i $- | ||
| + | th pair of opposite $ ( n - 1) $- | ||
| + | dimensional faces. See [[#References|[24]]], [[#References|[25]]] for more details. | ||
| − | In the theory of minimal surfaces and surfaces like them, a number of isoperimetric inequalities have been obtained that hold not only for smooth | + | In the theory of minimal surfaces and surfaces like them, a number of isoperimetric inequalities have been obtained that hold not only for smooth $ k $- |
| + | dimensional submanifolds in $ \mathbf R ^ {n} $, | ||
| + | $ n \geq k \geq 2 $, | ||
| + | but also for more general $ k $- | ||
| + | dimensional "films" : submanifolds with singularities, currents, etc. Thus, the following inequality was established in [[#References|[26]]], [[#References|[27]]]: | ||
| − | + | $$ \tag{5 } | |
| + | V \leq C ( k) ( F + H) ^ {k/( k - 1) } , | ||
| + | $$ | ||
| − | where | + | where $ F $ |
| + | is the $ ( k - 1) $- | ||
| + | area of a face and $ H $ | ||
| + | is the integral of the modulus of the mean curvature $ h $ | ||
| + | of the film. If $ k = 2 $, | ||
| + | then the following isoperimetric inequality holds when $ \alpha = 2 - \max | h | \mathop{\rm diam} H > 0 $: | ||
| − | + | $$ | |
| + | 4 \pi V \leq ( 1 - \alpha ) ^ {-} 1 F ^ { 2 } . | ||
| + | $$ | ||
| − | In methods of proof and applications, lower bounds for the volume | + | In methods of proof and applications, lower bounds for the volume $ V ( t) $ |
| + | of the intersection of a $ k $- | ||
| + | film $ M $ | ||
| + | with the ball of radius $ t $ | ||
| + | and centre at $ p \in M $ | ||
| + | belong to the class of inequalities of the type (5). Thus, for a minimal surface $ M $ | ||
| + | the function $ g ^ {-} k V ( t) $ | ||
| + | increases for all $ t < d ( x , \partial M) $. | ||
| + | See [[#References|[27]]], [[#References|[28]]] for some generalizations to minimal films in $ V ^ {n} $( | ||
| + | and to films under the assumption that $ | h | \leq \textrm{ const } $). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Bottema, "Geometric inequalities" , Noordhoff (1969) {{MR|0262932}} {{ZBL|0174.52401}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) {{MR|0102775}} {{ZBL|0078.35703}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934) {{MR|0344997}} {{MR|0372748}} {{MR|1512278}} {{ZBL|0008.07708}} {{ZBL|60.0673.01}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , ''Convexity'' , ''Proc. Symp. Pure Math.'' , '''7''' , Amer. Math. Soc. (1963) pp. 101–180 {{MR|157289}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.S. Mel'nikov, "On the relation between volume and diameter of sets in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052860/i052860155.png" />-dimensional Banach space" ''Uspekhi Mat. Nauk'' , '''18''' : 4 (1963) pp. 165–170 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) {{MR|}} {{ZBL|0229.52009}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951) {{MR|0043486}} {{ZBL|0044.38301}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.E. Payne, "Isoperimetric inequalities and their applications" ''Siam Rev.'' , '''9''' : 3 (1967) pp. 453–488 {{MR|0218975}} {{ZBL|0154.12602}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M. Berger, P. Ganduchon, E. Mazet, "Le spectre d'une variété riemannienne" , Springer (1971) {{MR|0282313}} {{ZBL|}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.G. Maz'ya, "Certain integral inequalities for functions of several variables" , ''Problems in mathematical analysis'' , '''3''' , Leningrad (1972) pp. 33–68 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.G. Maz'ya, "Classes of sets and measures connected with imbedding theorems" , ''Imbedding theorems and their applications'' , Moscow (1970) pp. 142–159 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.G. Maz'ya, "On weak solutions of the Dirichlet and Neumann problems" ''Trans. Moscow Math. Soc.'' , '''20''' (1969) pp. 135–172 ''Trudy Moskov. Mat. Obshch.'' , '''20''' (1969) pp. 137–172 {{MR|}} {{ZBL|0226.35027}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.D. Aleksandrov, V.V. Strel'tsov, "Isoperimetric problem and estimates of the length of a curve on a surface" ''Proc. Steklov Inst. Math.'' , '''76''' (1965) pp. 81–99 ''Trudy Mat. Inst. Steklov.'' , '''76''' (1965) pp. 67–80 {{MR|}} {{ZBL|0162.25903}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> Yu.D. Burago, "Note on the isoperimetric inequality on two-dimensional surfaces" ''Siberian Math. J.'' , '''14''' : 3 (1973) pp. 463–465 ''Sibirsk. Mat. Zh.'' , '''14''' : 3 (1973) pp. 666–668 {{MR|}} {{ZBL|0281.52005}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> J.K. Shahin, "Some integral formulas for closed hypersurfaces in Euclidean space" ''Proc. Amer. Math. Soc.'' , '''19''' : 3 (1968) pp. 609–613 {{MR|0227906}} {{ZBL|0165.24304}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> Yu.D. Burago, "Isoperimetric inequalities in the theory of surfaces of bounded external curvature" , Consultants Bureau (1970) (Translated from Russian) {{MR|0276905}} {{ZBL|0198.55001}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) {{MR|0169148}} {{ZBL|0132.16003}} </TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> J. Cheeger, "Finiteness theorems for Riemannian manifolds" ''Amer. J. Math.'' , '''92''' : 1 (1970) pp. 61–74 {{MR|0263092}} {{ZBL|0194.52902}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> G.A. Margulis, "Thesis" , ''VI All-Union Topological Conference'' , Tbilisi (1972) (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> B.V. Dekster, "Estimates of the volume of a region in a Riemannian space" ''Math. USSR Sb.'' , '''17''' : 1 (1972) pp. 61–87 ''Mat. Sb.'' , '''88''' : 1 (1972) pp. 61–87 {{MR|}} {{ZBL|0251.53047}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> Yu.A. Volkov, B.V. Dekster, "Estimates of the curvature of a three-dimensional evolute" ''Math. USSR Sb.'' , '''12''' : 4 (1970) pp. 615–640 ''Mat. Sb.'' , '''83''' : 4 (1970) pp. 616–638 {{MR|0275337}} {{ZBL|0219.53055}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> M. Berger, "Du côté de chez Pu" ''Ann. Sci. École Norm Sup. Sér. 4'' , '''5''' : 1 (1972) pp. 1–44 {{MR|0309008}} {{ZBL|0227.52005}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> M. Berger, "A l'ombre de Loewner" ''Ann. Sci. École Norm. Sup. Sér. 4'' , '''5''' : 2 (1972) pp. 241–260 {{MR|0309009}} {{ZBL|}} </TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> W.R. Derrick, "A weighted volume-diameter inequality for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052860/i052860156.png" />-cubes" ''J. Math. Mech.'' , '''18''' : 5 (1968) pp. 453–472 {{MR|246204}} {{ZBL|}} </TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> F. Almgren, "An isoperimetric inequality" ''Proc. Amer. Math. Soc.'' , '''15''' : 2 (1964) pp. 284–285 {{MR|0159925}} {{ZBL|0187.31203}} </TD></TR><TR><TD valign="top">[26]</TD> <TD valign="top"> J. Michael, L. Simon, "Sobolev and mean-value inequalities on generalized submanifolds of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052860/i052860157.png" />" ''Comm. Pure Appl. Math.'' , '''26''' : 23 (1973) pp. 361–379 {{MR|0344978}} {{ZBL|}} </TD></TR><TR><TD valign="top">[27]</TD> <TD valign="top"> W. Allard, "On the first variation of a varifold" ''Ann. of Math.'' , '''95''' (1972) pp. 417–491 {{MR|0307015}} {{ZBL|0252.49028}} </TD></TR><TR><TD valign="top">[28]</TD> <TD valign="top"> A.T. Fomenko, "Minimal compacta in Riemannian manifolds and a conjecture of Reifenberg" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''36''' : 5 (1972) pp. 1049–1079 (In Russian) {{MR|0333901}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Bottema, "Geometric inequalities" , Noordhoff (1969) {{MR|0262932}} {{ZBL|0174.52401}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) {{MR|0102775}} {{ZBL|0078.35703}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934) {{MR|0344997}} {{MR|0372748}} {{MR|1512278}} {{ZBL|0008.07708}} {{ZBL|60.0673.01}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , ''Convexity'' , ''Proc. Symp. Pure Math.'' , '''7''' , Amer. Math. Soc. (1963) pp. 101–180 {{MR|157289}} {{ZBL|}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.S. Mel'nikov, "On the relation between volume and diameter of sets in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052860/i052860155.png" />-dimensional Banach space" ''Uspekhi Mat. Nauk'' , '''18''' : 4 (1963) pp. 165–170 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) {{MR|}} {{ZBL|0229.52009}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951) {{MR|0043486}} {{ZBL|0044.38301}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.E. Payne, "Isoperimetric inequalities and their applications" ''Siam Rev.'' , '''9''' : 3 (1967) pp. 453–488 {{MR|0218975}} {{ZBL|0154.12602}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M. Berger, P. Ganduchon, E. Mazet, "Le spectre d'une variété riemannienne" , Springer (1971) {{MR|0282313}} {{ZBL|}} </TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> V.G. Maz'ya, "Certain integral inequalities for functions of several variables" , ''Problems in mathematical analysis'' , '''3''' , Leningrad (1972) pp. 33–68 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.G. Maz'ya, "Classes of sets and measures connected with imbedding theorems" , ''Imbedding theorems and their applications'' , Moscow (1970) pp. 142–159 (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> V.G. Maz'ya, "On weak solutions of the Dirichlet and Neumann problems" ''Trans. Moscow Math. Soc.'' , '''20''' (1969) pp. 135–172 ''Trudy Moskov. Mat. Obshch.'' , '''20''' (1969) pp. 137–172 {{MR|}} {{ZBL|0226.35027}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.D. Aleksandrov, V.V. Strel'tsov, "Isoperimetric problem and estimates of the length of a curve on a surface" ''Proc. Steklov Inst. Math.'' , '''76''' (1965) pp. 81–99 ''Trudy Mat. Inst. Steklov.'' , '''76''' (1965) pp. 67–80 {{MR|}} {{ZBL|0162.25903}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> Yu.D. Burago, "Note on the isoperimetric inequality on two-dimensional surfaces" ''Siberian Math. J.'' , '''14''' : 3 (1973) pp. 463–465 ''Sibirsk. Mat. Zh.'' , '''14''' : 3 (1973) pp. 666–668 {{MR|}} {{ZBL|0281.52005}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> J.K. Shahin, "Some integral formulas for closed hypersurfaces in Euclidean space" ''Proc. Amer. Math. Soc.'' , '''19''' : 3 (1968) pp. 609–613 {{MR|0227906}} {{ZBL|0165.24304}} </TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> Yu.D. Burago, "Isoperimetric inequalities in the theory of surfaces of bounded external curvature" , Consultants Bureau (1970) (Translated from Russian) {{MR|0276905}} {{ZBL|0198.55001}} </TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) {{MR|0169148}} {{ZBL|0132.16003}} </TD></TR><TR><TD valign="top">[18]</TD> <TD valign="top"> J. Cheeger, "Finiteness theorems for Riemannian manifolds" ''Amer. J. Math.'' , '''92''' : 1 (1970) pp. 61–74 {{MR|0263092}} {{ZBL|0194.52902}} </TD></TR><TR><TD valign="top">[19]</TD> <TD valign="top"> G.A. Margulis, "Thesis" , ''VI All-Union Topological Conference'' , Tbilisi (1972) (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[20]</TD> <TD valign="top"> B.V. Dekster, "Estimates of the volume of a region in a Riemannian space" ''Math. USSR Sb.'' , '''17''' : 1 (1972) pp. 61–87 ''Mat. Sb.'' , '''88''' : 1 (1972) pp. 61–87 {{MR|}} {{ZBL|0251.53047}} </TD></TR><TR><TD valign="top">[21]</TD> <TD valign="top"> Yu.A. Volkov, B.V. Dekster, "Estimates of the curvature of a three-dimensional evolute" ''Math. USSR Sb.'' , '''12''' : 4 (1970) pp. 615–640 ''Mat. Sb.'' , '''83''' : 4 (1970) pp. 616–638 {{MR|0275337}} {{ZBL|0219.53055}} </TD></TR><TR><TD valign="top">[22]</TD> <TD valign="top"> M. Berger, "Du côté de chez Pu" ''Ann. Sci. École Norm Sup. Sér. 4'' , '''5''' : 1 (1972) pp. 1–44 {{MR|0309008}} {{ZBL|0227.52005}} </TD></TR><TR><TD valign="top">[23]</TD> <TD valign="top"> M. Berger, "A l'ombre de Loewner" ''Ann. Sci. École Norm. Sup. Sér. 4'' , '''5''' : 2 (1972) pp. 241–260 {{MR|0309009}} {{ZBL|}} </TD></TR><TR><TD valign="top">[24]</TD> <TD valign="top"> W.R. Derrick, "A weighted volume-diameter inequality for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052860/i052860156.png" />-cubes" ''J. Math. Mech.'' , '''18''' : 5 (1968) pp. 453–472 {{MR|246204}} {{ZBL|}} </TD></TR><TR><TD valign="top">[25]</TD> <TD valign="top"> F. Almgren, "An isoperimetric inequality" ''Proc. Amer. Math. Soc.'' , '''15''' : 2 (1964) pp. 284–285 {{MR|0159925}} {{ZBL|0187.31203}} </TD></TR><TR><TD valign="top">[26]</TD> <TD valign="top"> J. Michael, L. Simon, "Sobolev and mean-value inequalities on generalized submanifolds of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i052/i052860/i052860157.png" />" ''Comm. Pure Appl. Math.'' , '''26''' : 23 (1973) pp. 361–379 {{MR|0344978}} {{ZBL|}} </TD></TR><TR><TD valign="top">[27]</TD> <TD valign="top"> W. Allard, "On the first variation of a varifold" ''Ann. of Math.'' , '''95''' (1972) pp. 417–491 {{MR|0307015}} {{ZBL|0252.49028}} </TD></TR><TR><TD valign="top">[28]</TD> <TD valign="top"> A.T. Fomenko, "Minimal compacta in Riemannian manifolds and a conjecture of Reifenberg" ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''36''' : 5 (1972) pp. 1049–1079 (In Russian) {{MR|0333901}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 22:13, 5 June 2020
(in geometry and physics)
A general term referring to the inequality $ 4 \pi V \leq F ^ { 2 } $ between the area $ V $ and perimeter $ F $ of a plane domain, to its various generalizations and to other inequalities between geometrical characteristics of figures, sets and manifolds. Also belonging to the general area of isoperimetric inequalities are estimates for quantities of physical origin (moments of inertia, torsional rigidity of an elastic beam, fundamental frequency of a membrane, electrostatic capacity, etc.) in terms of geometrical characteristics. An exact isoperimetric inequality is equivalent to the solution of some extremum problem. Isoperimetric inequalities can connect two or more quantities.
For the best known isoperimetric inequalities, namely the classical one and its analogues in the Minkowski spaces $ M ^ {n} $, the Lobachevskii spaces $ L ^ {n} $, the spheres $ S ^ {n} $, as well as for refinements of them, see Isoperimetric inequality, classical.
An extensive coverage of isoperimetric inequalities between the elements of the simplest figures, mainly polygons, can be found in [1]. Such isoperimetric inequalities are called geometric inequalities.
For elementary isoperimetric inequalities between such parameters of sets in $ \mathbf R ^ {n} $ as the volume $ V $, the diameter $ D $ and the radius $ R $ of the smallest circumscribed ball, etc., see [2] and [3]. Among them are: Young's inequality:
$$ R \leq \left ( { \frac{n}{2n + 2 } } \right ) ^ {1/2} D; $$
Gale's inequality:
$$ l \leq \left ( { \frac{n ( n + 1) }{2} } \right ) ^ {1/2} D, $$
where $ l $ is the length of the edge of the smallest circumscribed regular simplex; Bieberbach's inequality:
$$ V \leq 2 ^ {-} n V _ {n} D ^ {n} ; $$
and the Loomis–Whitney inequality:
$$ V \leq \ \prod _ {i = 1 } ^ \lambda V _ {i} ^ {n/k \lambda } , $$
where $ V _ {i} $ is the $ k $- dimensional volume of the projection of the set onto the $ i $- th of the $ \lambda = ( {} _ {k} ^ {n} ) $ pairwise-different $ k $- dimensional Cartesian coordinate planes. The first three inequalities can be generalized to the spaces $ M ^ {n} $, $ L ^ {n} $, $ S ^ {n} $( see [4], [5]). In Bieberbach's inequality, the diameter can be replaced by the mean width (see [5]).
In connection with problems of arrangement and covering, isoperimetric inequalities are considered that are specific for polyhedra, with the introduction of the number of edges or the sum of their lengths, etc. (see [6]).
For convex bodies, many isoperimetric inequalities (including the classical ones and a number of inequalities between integrals of symmetric functions of principal curvatures) are special cases of inequalities between composite objects (see Mixed-volume theory; Minkowski inequality).
The use of isoperimetric inequalities as estimates for some parameters of figures in terms of others arose within the limits of geometry. The class of isoperimetric inequalities is enriched by mathematical physics, the theory of functions of a complex variable, functional analysis, the theory of approximations of functions, and the calculus of variations. Isoperimetric inequalities in Riemannian geometry are noticeably more complex.
In mathematical physics, isoperimetric inequalities arose (firstly as conjectures) in papers of A. Saint-Venant (1856):
$$ 2 \pi P \leq V ^ {2} , $$
where $ P $ is the torsional rigidity of a prismatic elastic beam; of Lord Rayleigh (1877):
$$ \Lambda ^ {2} \leq \pi j ^ {2} V ^ {-} 1 , $$
where $ \Lambda $ is the fundamental frequency of the membrane and $ j $ is the first positive root of the Bessel function $ J _ {0} ( x) $; and in papers of H. Poincaré (1903):
$$ 3V \leq 4 \pi c ^ {3} , $$
where $ c $ is the electrostatic capacity of the body. In these inequalities, $ V $ is, respectively, the cross-sectional area of the beam, the area of the membrane and the volume of the body. Numerous results of this sort are summarized in [7] and [8]. Certain estimates for the first eigen value $ \Lambda ^ {-} 1 $ of the Laplace operator on closed Riemannian manifolds can be found in [9].
In functional analysis, conditions for boundedness and compactness of imbedding operators (see Imbedding theorems) for Sobolev spaces have been given in terms of isoperimetric inequalities (connecting measure and capacity) (see [10], [11]).
For example, the estimate
$$ \left ( \int\limits _ {\mathbf R ^ {n} } | u | ^ {q} d \mu \right ) ^ {n/q} \leq \ c \int\limits _ {\mathbf R ^ {n} } ( \nabla u) ^ {2} dx, $$
where $ \mu $ is a non-negative measure, $ q \geq 2 $, $ n > 2 $, is valid for all $ u \in C _ {0} ^ \infty ( \mathbf R ^ {n} ) $ if and only if the following isoperimetric inequality is satisfied for all compacta $ e \subset \mathbf R ^ {n} $:
$$ \mu ^ {2/q} ( e) \leq c _ {1} \mathop{\rm cap} ( e). $$
Here $ \mathop{\rm cap} ( \cdot ) $ is the Wiener capacity (see Capacity).
Isoperimetric inequalities for volume and area are used in the proof of a priori estimates for solutions of linear and quasi-linear elliptic equations (see [12], [26]).
Specific isoperimetric inequalities arise for convex bodies in a Minkowski space in connection with the theory of approximation of functions (see Self-perimeter; Width).
Applying isoperimetric inequalities is a standard device in the theory of conformal and quasi-conformal mappings. Inequality (4) below is an example of a conformally-invariant isoperimetric inequality.
Isoperimetric inequalities involving the mean curvature of a submanifold, in particular for minimal surfaces, play an important part in the solution of the Plateau problem.
In the Riemannian geometry of non-homogeneous spaces, generalizations of the classical isoperimetric inequalities have been studied in detail only in the two-dimensional case. Let $ M $ be a simply-connected compact two-dimensional manifold with boundary such that the positive part $ \omega ^ {+} $ of the integral curvature of $ M $ is less than $ 2 \pi $. Then (see [13]):
$$ \tag{1 } 2 ( 2 \pi - \omega ^ {+} ) V \leq F ^ { 2 } . $$
The isoperimetric inequality (1) is valid also for a two-dimensional manifold of bounded curvature, which is a more general type of manifold than a Riemannian manifold. Equality in (1) is attained for a non-regular object — a domain isometric to the lateral surface of a right circular cone with complete angle $ 2 \pi - \omega ^ {+} $ about the vertex. Using (1), inequalities can be established for the length of a curve, inside the domain, in dependence on $ F $, $ \omega ^ {+} $ and the proper rotation (cf. Winding number). In particular, for the geodesic length $ L $,
$$ L \left ( 1 + \cos { \frac{1}{2} } \omega ^ {+} \right ) \leq F \ \ \textrm{ if } \omega ^ {+} \leq \pi , $$
$$ L \sin { \frac{1}{2} } \omega ^ {+} \leq F \ \textrm{ if } \pi \leq \omega ^ {+} < 2 \pi . $$
Isoperimetric inequality (1) is a special case of the estimate
$$ \tag{2 } F ^ { 2 } + 2 ( \omega _ {a} ^ {+} - 2 \pi \chi ) V + aV \geq 0, $$
where $ a $ is any real number, $ \chi $ is the Euler characteristic of the compact domain with boundary, $ \omega ^ {+} = \int ( K - a) ^ {+} dV $, and $ K $ is the Gaussian curvature. Similar to (2) are estimates for the area of a $ t $- neighbourhood of the boundary of a domain and for the largest distance of points in the domain from the boundary (see [14]). If the surface $ M $ is a smooth submanifold in $ \mathbf R ^ {3} $, then the estimates (1), (2) are supplemented by isoperimetric inequalities involving the external characteristics of the surface. For closed surfaces, the following sharp isoperimetric inequality follows from integral identities (see [15]):
$$ V \leq 2R ^ {2} ( \omega ^ {+} - \pi \chi ), $$
where $ R $ is the radius of a ball in $ \mathbf R ^ {3} $ containing $ M $. Similar (but non-sharp) inequalities have been obtained also for surfaces with boundary (see [16]). In particular, for a simply-connected saddle surface in $ \mathbf R ^ {n} $ with boundary length $ F $:
$$ V \leq CF ^ { 2 } ,\ \ V \leq CF ^ { 2 - \epsilon } R ^ \epsilon , $$
$$ { \frac{1}{7} } > \epsilon = \textrm{ const } > 0. $$
The inequalities mentioned remain true for general (non-regular) surfaces in $ \mathbf R ^ {n} $, $ n \geq 2 $, if instead of $ \omega ^ {+} $ the positive exterior curvature is taken into consideration — a measure in the set of locally supporting planes (see [16]).
For an $ n $- dimensional Riemannian space $ V ^ {n} $, isoperimetric inequalities are usually connected with one-sided bounds on the sectional curvature or the Ricci curvature. The simplest is a bound for the volume $ V ( t) $ of the ball of radius $ t $ in $ V ^ {n} $ in terms of the volume $ v ( t, K) $ of a ball of the same radius in a complete simply-connected surface of constant curvature $ K $:
$$ \tag{3 } V ( t) \leq v ( t, K), $$
where $ ( n - 1) K $ is the smallest value of the Ricci curvature in $ V ^ {n} $; if $ K > 0 $, then it is assumed that $ t \leq \pi / \sqrt K $( see [17]). Similar isoperimetric inequalities are valid for a tubular $ t $- neighbourhood of a $ p $- dimensional submanifold of $ V ^ {n} $, $ 0 \leq p < n $; the minimum of the sectional curvatures in $ V ^ {n} $ and the maximum of the normal curvatures of submanifolds participate in such an isoperimetric inequality (instead of the Ricci curvature) (see [18]).
If the least upper bound $ \overline{K}\; $ of the sectional curvatures is negative, then the volume $ V $ of the closed manifold is bounded from below by $ \overline{K}\; $( see [19]). The following linear isoperimetric inequality holds for a domain $ M $ in a complete simply-connected $ V ^ {n} $:
$$ ( n - 1) \sqrt {- K } V \leq F, $$
where $ F $ is the $ ( n - 1) $- dimensional area of the boundary of $ M $, and also the isoperimetric inequality
$$ V ^ {( n - 1)/n } \leq c ( n) F, $$
the exact value of $ c ( n) $ being unknown.
In spaces of negative curvature, a number of estimates have been obtained for convex domains that generalize isoperimetric inequalities for convex bodies in $ \mathbf R ^ {n} $( see [20], [21]). Thus,
$$ n ^ {-} 1 rF \leq V \leq rF, $$
where $ r $ is the greatest distance of points of $ M $ from the boundary. If the greatest lower bound $ \underline{K} $ of the sectional curvatures in $ M $ is positive, then $ r \sqrt {\underline{K} } < \pi $, and the left inequality can be sharpened:
$$ F \sin ^ {1/n} r \sqrt {\underline{K} } \int\limits _ { 0 } ^ { r } \sin ^ {n - 1 } t \sqrt {\underline{K} } \ dt \leq V. $$
The inequality $ rH \leq F $ holds, where $ H $ is the integral mean curvature. The following isoperimetric inequality holds in the three-dimensional case:
$$ 2 \pi \chi r \leq H + \Omega , $$
where $ \chi $ is the Euler characteristic of the boundary of $ M $ and $ \Omega $ is the integral scalar curvature of $ M $.
In the classical isoperimetric inequality, the area is bounded from above. For closed simply-connected surfaces, the area can be bounded from below in terms of the length $ \lambda $ of the shortest loop that is not homotopic to zero:
$$ \tag{4 } \lambda ^ {2} c ( \chi ) \leq V. $$
The exact value of $ c ( \chi ) $ is known only for the torus $ ( = \sqrt 3 /2) $ and the projective plane $ ( = 2/ \pi ) $. Inequality (4) is a corollary of the following isoperimetric inequality (see [22]):
$$ \tag{4'} \lambda _ {e} \leq C ^ {-} 1 ( \chi ) $$
for the extremal length $ \lambda _ {e} $ of the family of loops that are not homotopic to zero.
The problem of similar inequalities for $ V ^ {n} $ with $ n > 2 $ is discussed in [22]. If $ M $ is a topological $ n $- dimensional cube with interior metric $ g $, then its $ n $- volume satisfies the inequality
$$ V \geq \prod _ {i = 1 } ^ { n } g _ {i} ; $$
here $ g _ {i} $ is the distance in the metric $ g $ between the $ i $- th pair of opposite $ ( n - 1) $- dimensional faces. See [24], [25] for more details.
In the theory of minimal surfaces and surfaces like them, a number of isoperimetric inequalities have been obtained that hold not only for smooth $ k $- dimensional submanifolds in $ \mathbf R ^ {n} $, $ n \geq k \geq 2 $, but also for more general $ k $- dimensional "films" : submanifolds with singularities, currents, etc. Thus, the following inequality was established in [26], [27]:
$$ \tag{5 } V \leq C ( k) ( F + H) ^ {k/( k - 1) } , $$
where $ F $ is the $ ( k - 1) $- area of a face and $ H $ is the integral of the modulus of the mean curvature $ h $ of the film. If $ k = 2 $, then the following isoperimetric inequality holds when $ \alpha = 2 - \max | h | \mathop{\rm diam} H > 0 $:
$$ 4 \pi V \leq ( 1 - \alpha ) ^ {-} 1 F ^ { 2 } . $$
In methods of proof and applications, lower bounds for the volume $ V ( t) $ of the intersection of a $ k $- film $ M $ with the ball of radius $ t $ and centre at $ p \in M $ belong to the class of inequalities of the type (5). Thus, for a minimal surface $ M $ the function $ g ^ {-} k V ( t) $ increases for all $ t < d ( x , \partial M) $. See [27], [28] for some generalizations to minimal films in $ V ^ {n} $( and to films under the assumption that $ | h | \leq \textrm{ const } $).
References
| [1] | O. Bottema, "Geometric inequalities" , Noordhoff (1969) MR0262932 Zbl 0174.52401 |
| [2] | H. Hadwiger, "Vorlesungen über Inhalt, Oberfläche und Isoperimetrie" , Springer (1957) MR0102775 Zbl 0078.35703 |
| [3] | T. Bonnesen, W. Fenchel, "Theorie der konvexen Körper" , Springer (1934) MR0344997 MR0372748 MR1512278 Zbl 0008.07708 Zbl 60.0673.01 |
| [4] | L. Danzer, B. Grünbaum, V.L. Klee, "Helly's theorem and its relatives" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 101–180 MR157289 |
| [5] | M.S. Mel'nikov, "On the relation between volume and diameter of sets in  -dimensional Banach space" Uspekhi Mat. Nauk , 18 : 4 (1963) pp. 165–170 (In Russian) -dimensional Banach space" Uspekhi Mat. Nauk , 18 : 4 (1963) pp. 165–170 (In Russian) |
| [6] | L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) Zbl 0229.52009 |
| [7] | G. Pólya, G. Szegö, "Isoperimetric inequalities in mathematical physics" , Princeton Univ. Press (1951) MR0043486 Zbl 0044.38301 |
| [8] | L.E. Payne, "Isoperimetric inequalities and their applications" Siam Rev. , 9 : 3 (1967) pp. 453–488 MR0218975 Zbl 0154.12602 |
| [9] | M. Berger, P. Ganduchon, E. Mazet, "Le spectre d'une variété riemannienne" , Springer (1971) MR0282313 |
| [10] | V.G. Maz'ya, "Certain integral inequalities for functions of several variables" , Problems in mathematical analysis , 3 , Leningrad (1972) pp. 33–68 (In Russian) |
| [11] | V.G. Maz'ya, "Classes of sets and measures connected with imbedding theorems" , Imbedding theorems and their applications , Moscow (1970) pp. 142–159 (In Russian) |
| [12] | V.G. Maz'ya, "On weak solutions of the Dirichlet and Neumann problems" Trans. Moscow Math. Soc. , 20 (1969) pp. 135–172 Trudy Moskov. Mat. Obshch. , 20 (1969) pp. 137–172 Zbl 0226.35027 |
| [13] | A.D. Aleksandrov, V.V. Strel'tsov, "Isoperimetric problem and estimates of the length of a curve on a surface" Proc. Steklov Inst. Math. , 76 (1965) pp. 81–99 Trudy Mat. Inst. Steklov. , 76 (1965) pp. 67–80 Zbl 0162.25903 |
| [14] | Yu.D. Burago, "Note on the isoperimetric inequality on two-dimensional surfaces" Siberian Math. J. , 14 : 3 (1973) pp. 463–465 Sibirsk. Mat. Zh. , 14 : 3 (1973) pp. 666–668 Zbl 0281.52005 |
| [15] | J.K. Shahin, "Some integral formulas for closed hypersurfaces in Euclidean space" Proc. Amer. Math. Soc. , 19 : 3 (1968) pp. 609–613 MR0227906 Zbl 0165.24304 |
| [16] | Yu.D. Burago, "Isoperimetric inequalities in the theory of surfaces of bounded external curvature" , Consultants Bureau (1970) (Translated from Russian) MR0276905 Zbl 0198.55001 |
| [17] | R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964) MR0169148 Zbl 0132.16003 |
| [18] | J. Cheeger, "Finiteness theorems for Riemannian manifolds" Amer. J. Math. , 92 : 1 (1970) pp. 61–74 MR0263092 Zbl 0194.52902 |
| [19] | G.A. Margulis, "Thesis" , VI All-Union Topological Conference , Tbilisi (1972) (In Russian) |
| [20] | B.V. Dekster, "Estimates of the volume of a region in a Riemannian space" Math. USSR Sb. , 17 : 1 (1972) pp. 61–87 Mat. Sb. , 88 : 1 (1972) pp. 61–87 Zbl 0251.53047 |
| [21] | Yu.A. Volkov, B.V. Dekster, "Estimates of the curvature of a three-dimensional evolute" Math. USSR Sb. , 12 : 4 (1970) pp. 615–640 Mat. Sb. , 83 : 4 (1970) pp. 616–638 MR0275337 Zbl 0219.53055 |
| [22] | M. Berger, "Du côté de chez Pu" Ann. Sci. École Norm Sup. Sér. 4 , 5 : 1 (1972) pp. 1–44 MR0309008 Zbl 0227.52005 |
| [23] | M. Berger, "A l'ombre de Loewner" Ann. Sci. École Norm. Sup. Sér. 4 , 5 : 2 (1972) pp. 241–260 MR0309009 |
| [24] | W.R. Derrick, "A weighted volume-diameter inequality for  -cubes" J. Math. Mech. , 18 : 5 (1968) pp. 453–472 MR246204 -cubes" J. Math. Mech. , 18 : 5 (1968) pp. 453–472 MR246204 |
| [25] | F. Almgren, "An isoperimetric inequality" Proc. Amer. Math. Soc. , 15 : 2 (1964) pp. 284–285 MR0159925 Zbl 0187.31203 |
| [26] | J. Michael, L. Simon, "Sobolev and mean-value inequalities on generalized submanifolds of 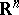 " Comm. Pure Appl. Math. , 26 : 23 (1973) pp. 361–379 MR0344978 " Comm. Pure Appl. Math. , 26 : 23 (1973) pp. 361–379 MR0344978 |
| [27] | W. Allard, "On the first variation of a varifold" Ann. of Math. , 95 (1972) pp. 417–491 MR0307015 Zbl 0252.49028 |
| [28] | A.T. Fomenko, "Minimal compacta in Riemannian manifolds and a conjecture of Reifenberg" Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 5 (1972) pp. 1049–1079 (In Russian) MR0333901 |
Comments
For an up-to-date account of geometric inequalities supplementing [1], see [a3].
References
| [a1] | C. Bandle, "Isoperimetric inequalities and applications" , Pitman (1980) MR0572958 Zbl 0436.35063 |
| [a2] | H. Kaul, "Isoperimetrische Ungleichung und Gauss–Bonnet–Formel für 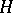 -Flächen in Riemannsche Mannigfaltigkeiten" Arch. Rat. Mech. Anal. , 45 (1972) pp. 194–221 -Flächen in Riemannsche Mannigfaltigkeiten" Arch. Rat. Mech. Anal. , 45 (1972) pp. 194–221 |
| [a3] | D.S. Mitrinović, J.E. Pečarić, V. Volenec, "Recent advances in geometric inequalities" , Kluwer (1989) MR1022443 Zbl 0679.51004 |
Isoperimetric inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isoperimetric_inequality&oldid=28222