Isomorphism
A correspondence (relation) between objects or systems of objects expressing the equality of their structures in some sense. An isomorphism in an arbitrary category is an invertible morphism, that is, a morphism  for which there exists a morphism
for which there exists a morphism  such that
such that  and
and  are both identity morphisms.
are both identity morphisms.
The concept of an isomorphism arose in connection with concrete algebraic systems (initially, with groups) and was extended in a natural way to wider classes of mathematical structures. A classical example of isomorphic, "identically constructed" , systems is the set  of real numbers with the operation of addition and the set
of real numbers with the operation of addition and the set  of positive real numbers with the operation of multiplication.
of positive real numbers with the operation of multiplication.
Let  and
and  be algebraic systems (cf. Algebraic system) of the same type, written in the signature
be algebraic systems (cf. Algebraic system) of the same type, written in the signature
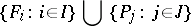 |
with function symbols  ,
,  , and predicate symbols
, and predicate symbols  ,
,  :
:
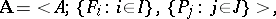 |
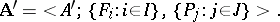 |
An isomorphism, or isomorphic mapping, from  onto
onto  is a one-to-one mapping
is a one-to-one mapping 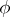 from the set
from the set  onto the set
onto the set  with the properties:
with the properties:
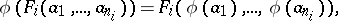 |
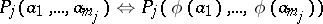 |
for all  in
in  and all
and all  ,
, 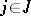 . Thus, in every category of algebraic systems, an isomorphism is a homomorphism that is a bijection. An isomorphism of an algebraic system onto itself is called an automorphism.
. Thus, in every category of algebraic systems, an isomorphism is a homomorphism that is a bijection. An isomorphism of an algebraic system onto itself is called an automorphism.
The relation of isomorphism is reflexive, symmetric and transitive, that is, it is an equivalence relation splitting any set on which it is defined into disjoint equivalence classes — the classes of pairwise-isomorphic systems. A class of algebraic systems which is a union of such classes is called an abstract class (cf. Algebraic systems, class of).
Comments
The isomorphism between  and
and  mentioned in the main article above can be explicitly given by the means of the exponential mapping or its inverse, the logarithmic function (cf. also Exponential function, real).
mentioned in the main article above can be explicitly given by the means of the exponential mapping or its inverse, the logarithmic function (cf. also Exponential function, real).
References
| [a1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [a2] | J. Adámek, "Theory of mathematical structures" , Reidel (1983) |
| [a3] | B. Mitchell, "Theory of categories" , Acad. Press (1965) pp. 7 |
Isomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isomorphism&oldid=12359