Isometric mapping
A mapping  from a metric space
from a metric space  into a metric space
into a metric space  preserving distances between points: If
preserving distances between points: If  and
and  , then
, then
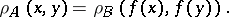 |
An isometric mapping is an injective mapping of a special type, indeed it is an immersion. If  , that is, if
, that is, if  is a bijection, then
is a bijection, then  is said to be an isometry from
is said to be an isometry from  onto
onto  , and
, and  and
and  are said to be in isometric correspondence, or to be isometric to each other. Isometric spaces are homeomorphic. If in addition
are said to be in isometric correspondence, or to be isometric to each other. Isometric spaces are homeomorphic. If in addition  is the same as
is the same as  , then the isometric mapping is said to be an isometric transformation, or a motion, of
, then the isometric mapping is said to be an isometric transformation, or a motion, of  .
.
If the metric spaces 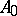 and
and 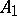 are subsets of some topological space
are subsets of some topological space 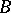 and if there exists a deformation
and if there exists a deformation 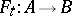 such that
such that 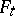 is an isometric mapping from
is an isometric mapping from 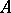 onto
onto 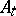 for each
for each  , then
, then 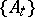 is called an isometric deformation of
is called an isometric deformation of 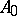 into
into  .
.
An isometry of real Banach spaces is an affine mapping. Such a linear isometry is realized by (and called) an isometric operator.
Comments
The fact that isometries of real Banach spaces are affine is due to S. Ulam and S. Mazur [a1].
References
| [a1] | S. Mazur, S. Ulam, "Sur les transformations isométriques d'espaces vectoriels" C.R. Acad. Sci. Paris , 194 (1932) pp. 946–948 |
Isometric mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isometric_mapping&oldid=15201