Isolated singular point
for an element of an analytic function 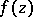
A point  in the complex
in the complex  -plane satisfying the following properties: 1) the element of
-plane satisfying the following properties: 1) the element of 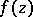 does not have an analytic continuation along any path to
does not have an analytic continuation along any path to  ; and 2) there exists a number
; and 2) there exists a number 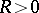 such that analytic continuation of
such that analytic continuation of 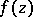 is possible along any path in the punctured neighbourhood
is possible along any path in the punctured neighbourhood 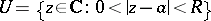 of
of  .
.
If a new element is obtained when 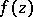 is continued analytically along a closed path in
is continued analytically along a closed path in 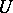 encircling
encircling  , for example along the circle
, for example along the circle 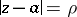 ,
, 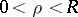 , then
, then  is called a branch point, or an isolated singular point of multi-valued character. Otherwise the element of
is called a branch point, or an isolated singular point of multi-valued character. Otherwise the element of 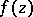 defines a single-valued analytic function in
defines a single-valued analytic function in 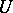 and
and  is called an isolated singular point of single-valued character. In a punctured neighbourhood
is called an isolated singular point of single-valued character. In a punctured neighbourhood 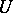 of an isolated singular point
of an isolated singular point  of single-valued character,
of single-valued character,  can be expanded in a Laurent series:
can be expanded in a Laurent series:
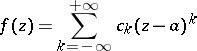 | (1) |
with regular part 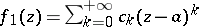 and principal part
and principal part 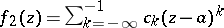 . The behaviour of an analytic function
. The behaviour of an analytic function 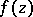 in a punctured neighbourhood
in a punctured neighbourhood 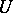 of an isolated singular point of single-valued character is determined, in principle, by the principal part of its Laurent series. If all the coefficients of the principal part are zero, then on setting
of an isolated singular point of single-valued character is determined, in principle, by the principal part of its Laurent series. If all the coefficients of the principal part are zero, then on setting 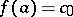 one gets a single-valued analytic function in a full neighbourhood of
one gets a single-valued analytic function in a full neighbourhood of  . This case of practical absence of a singularity is also characterized by the fact that
. This case of practical absence of a singularity is also characterized by the fact that 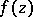 is bounded in
is bounded in 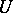 , or by the fact that the limit
, or by the fact that the limit 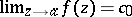 ,
, 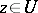 , exists and is finite.
, exists and is finite.
If among the coefficients of the principal part only finitely many are non-zero, and that with smallest index is 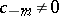 , then
, then  is a pole of order
is a pole of order 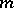 (cf. Pole (of a function)). A pole
(cf. Pole (of a function)). A pole  is also characterized by the fact that
is also characterized by the fact that
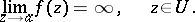 |
Finally, if there are infinitely many non-zero coefficients in the principal part, then  is an essential singular point. In this case the following limit does not exist, neither finite nor infinite:
is an essential singular point. In this case the following limit does not exist, neither finite nor infinite:
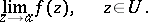 |
For an isolated singular point 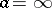 at infinity of the element
at infinity of the element 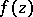 , a punctured neighbourhood has the form
, a punctured neighbourhood has the form 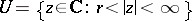 , and the Laurent series is
, and the Laurent series is
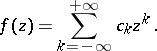 |
Here the regular part is 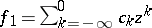 and the principal part is
and the principal part is 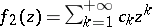 . With these conditions, the above descriptions of the classification and criteria for the type of an isolated singular point carry over to the case
. With these conditions, the above descriptions of the classification and criteria for the type of an isolated singular point carry over to the case 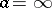 without further change (see also Residue of an analytic function). It should be noted that the elements of different branches of the complete analytic function
without further change (see also Residue of an analytic function). It should be noted that the elements of different branches of the complete analytic function 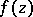 at one and the same point
at one and the same point 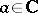 may have singularities of completely-different types.
may have singularities of completely-different types.
Holomorphic functions  of several complex variables
of several complex variables 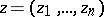 ,
, 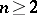 , cannot have isolated singular points. For
, cannot have isolated singular points. For  , the singular points form infinite sets of singularities.
, the singular points form infinite sets of singularities.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
References
| [a1] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
| [a2] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. 241 |
Isolated singular point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isolated_singular_point&oldid=12648