Isogonal trajectory
A plane curve intersecting the curves of a given one-parameter family in the plane at one and the same angle. If
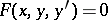 | (1) |
is the differential equation of the given family of curves, then an isogonal trajectory of this family intersecting it at an angle 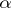 , where
, where 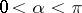 ,
, 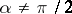 , satisfies one of the following two equations:
, satisfies one of the following two equations:
 |
In particular, the equation
 | (2) |
is satisfied by an orthogonal trajectory, that is, a plane curve that forms a right angle at each of its points with any curve of the family (1) passing through it. The orthogonal trajectories for the given system (1) form a one-parameter family of plane curves — the general integral of equation (1). For example, if the family of lines of force of a plane electrostatic field is considered, then the family of orthogonal trajectories are the equipotential lines.
References
| [1] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
References
| [a1] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
Isogonal trajectory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isogonal_trajectory&oldid=18698