Ising model
A model [a1] defined by the following Hamiltonian (cf. Hamilton function)  (i.e. energy functional of variables; in this case the "spins"
(i.e. energy functional of variables; in this case the "spins"  on the
on the  sites of a regular lattice in a space of dimension
sites of a regular lattice in a space of dimension  )
)
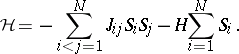 | (a1) |
Here,  are "exchange constants" ,
are "exchange constants" ,  is a (normalized) magnetic field, involving an interpretation of the model to describe magnetic ordering in solids (
is a (normalized) magnetic field, involving an interpretation of the model to describe magnetic ordering in solids ( is "magnetization" , the Zeeman energy
is "magnetization" , the Zeeman energy  in (a1) is the energy gained due to application of the field).
in (a1) is the energy gained due to application of the field).
Since its solution for 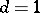 in 1925 [a1], the model became a "fruitfly" for the development of both concepts and techniques in statistical thermodynamics. It appears also in other interpretations in lattice statistics: defining occupation variables
in 1925 [a1], the model became a "fruitfly" for the development of both concepts and techniques in statistical thermodynamics. It appears also in other interpretations in lattice statistics: defining occupation variables 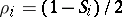 , where lattice site
, where lattice site 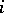 is empty (
is empty (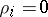 ) if
) if  or occupied (
or occupied (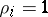 ) if
) if 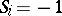 . This is the lattice gas model of a fluid. One can also interpret the cases
. This is the lattice gas model of a fluid. One can also interpret the cases 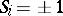 as two chemical species
as two chemical species 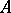 ,
,  for describing ordering or unmixing of binary alloys
for describing ordering or unmixing of binary alloys  , etc.
, etc.
Statistical thermodynamics [a2] aims to compute average properties of systems with a large number of degrees of freedom (i.e., in the thermodynamic limit 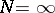 ). These averages at a temperature
). These averages at a temperature 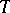 are obtained from the free energy
are obtained from the free energy  (per spin) or the partition function
(per spin) or the partition function 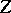 ,
,
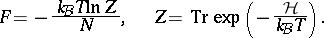 | (a2) |
Here, 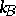 is the Boltzmann constant [a2], and the trace operation
is the Boltzmann constant [a2], and the trace operation 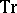 stands for a sum over all the states in the phase space of the system (which here is the set of
stands for a sum over all the states in the phase space of the system (which here is the set of 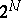 states
states 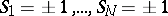 ). Magnetization per spin
). Magnetization per spin  , susceptibility
, susceptibility 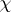 , entropy
, entropy  , etc. are then found as partial derivatives of
, etc. are then found as partial derivatives of 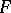 [a2]:
[a2]:
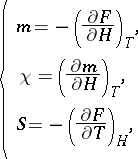 | (a3) |
where 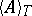 stands for a canonical average of a quantity
stands for a canonical average of a quantity 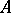 :
:
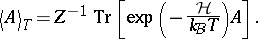 |
The Ising model is important since for 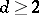 it exhibits phase transitions. In the simplest case,
it exhibits phase transitions. In the simplest case, 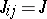 if sites
if sites  ,
,  are nearest neighbours on the lattice and zero elsewhere, a transition occurs for
are nearest neighbours on the lattice and zero elsewhere, a transition occurs for  from a paramagnet (
from a paramagnet (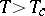 ) to a ferromagnet (
) to a ferromagnet ( ) at a critical temperature
) at a critical temperature 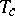 . In the disordered paramagnet
. In the disordered paramagnet 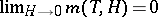 , while in the ordered ferromagnet the spontaneous magnetization
, while in the ordered ferromagnet the spontaneous magnetization 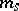 occurs:
occurs:
 | (a4) |
This is an example of spontaneous symmetry breaking: 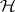 for
for 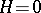 does not single out a sign of
does not single out a sign of 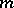 (replacing all
(replacing all 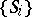 by
by 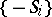 leaves
leaves  invariant). However, for
invariant). However, for 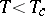 and
and 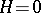 the equilibrium state of the system is two-fold degenerate (
the equilibrium state of the system is two-fold degenerate ( ). This degeneracy is already obvious from the groundstate of (a1), for
). This degeneracy is already obvious from the groundstate of (a1), for 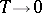 , found from the absolute minimum of
, found from the absolute minimum of  as a functional of the
as a functional of the  : for
: for 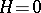 this minimum occurs for either all
this minimum occurs for either all 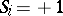 or all
or all 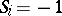 .
.
Interestingly, for  no such phase transition at
no such phase transition at 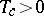 occurs; rather
occurs; rather  [a1]. The problem (a1)–(a3) is solved exactly by transfer matrix methods [a3]. Rewriting (a1) as
[a1]. The problem (a1)–(a3) is solved exactly by transfer matrix methods [a3]. Rewriting (a1) as 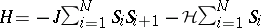 with the periodic boundary condition
with the periodic boundary condition 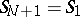 , one finds
, one finds
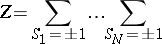 | (a5) |
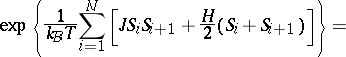 |
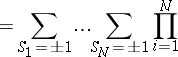 |
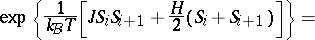 |
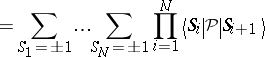 |
The 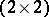 -matrix
-matrix  is defined as
is defined as
 | (a6) |
Now 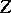 is simply the trace of an
is simply the trace of an  -fold matrix product,
-fold matrix product,
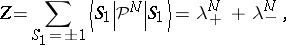 | (a7) |
where the property was used that the trace of a symmetric matrix is independent of the representation, and so one can evaluate the trace by first diagonalizing 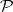 ,
,
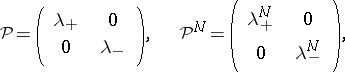 | (a8) |
where the eigenvalues  ,
, 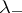 are found from the vanishing of the determinant,
are found from the vanishing of the determinant, 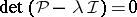 ,
,  being the unit
being the unit  -matrix:
-matrix:
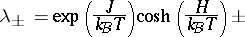 | (a9) |
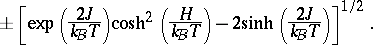 |
In the limit 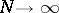 the largest eigenvalue dominates,
the largest eigenvalue dominates, 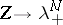 , and hence
, and hence
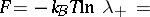 | (a10) |
 |
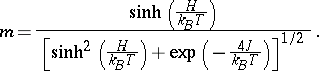 | (a11) |
Indeed, for  there is no spontaneous magnetization, and for
there is no spontaneous magnetization, and for 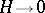 the susceptibility becomes
the susceptibility becomes 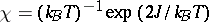 .
.
It is remarkable that (a11) strongly contradicts the popular molecular field approximation (MFA). In the molecular field approximation one replaces in the interaction of every spin 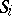 with its neighbours,
with its neighbours,  , the spins by their averages,
, the spins by their averages, 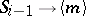 ;
; 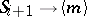 , the problem becomes a single-site Hamiltonian where
, the problem becomes a single-site Hamiltonian where  is exposed to an effective field
is exposed to an effective field  , which needs to be calculated self-consistently; carrying out the average over the two states
, which needs to be calculated self-consistently; carrying out the average over the two states 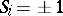 one finds
one finds
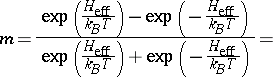 | (a12) |
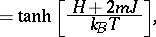 |
which yields 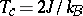 and
and 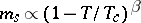 with a critical exponent
with a critical exponent 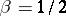 , and a Curie–Weiss law for
, and a Curie–Weiss law for 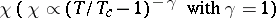 . Thus, the Ising model shows that the molecular field approximation in this case yields unreliable and misleading results!
. Thus, the Ising model shows that the molecular field approximation in this case yields unreliable and misleading results!
For the Ising-model in 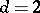 , exact transfer matrix methods are applicable for
, exact transfer matrix methods are applicable for 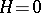 ; they show that a phase transition at
; they show that a phase transition at 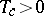 does exist [a3], [a4], [a5]. But the critical exponents
does exist [a3], [a4], [a5]. But the critical exponents  ,
, 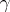 differ very much from their molecular field approximation values; namely,
differ very much from their molecular field approximation values; namely, 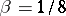 and
and 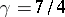 . This is important, since the exponents
. This is important, since the exponents 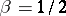 and
and 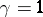 also follow from the Landau theory of phase transitions [a2], which only requires that
also follow from the Landau theory of phase transitions [a2], which only requires that  can be expanded in a power series in
can be expanded in a power series in 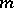 , with the coefficient at the
, with the coefficient at the 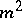 term changing sign at
term changing sign at  as
as 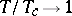 , which are plausible assumptions on many grounds. The
, which are plausible assumptions on many grounds. The 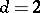 Ising model testifies that neither molecular field approximation nor Landau theory are correct. The Ising model then prompted the development of entirely new theoretical concepts, namely renormalization group analysis [a6], by which one can understand how non-mean-field critical behaviour arises. The Ising model also became a very useful testing ground for many numerical methods: e.g. systematic expansions of
Ising model testifies that neither molecular field approximation nor Landau theory are correct. The Ising model then prompted the development of entirely new theoretical concepts, namely renormalization group analysis [a6], by which one can understand how non-mean-field critical behaviour arises. The Ising model also became a very useful testing ground for many numerical methods: e.g. systematic expansions of 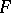 at low
at low 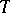 (in the variable
(in the variable  ) or at high
) or at high 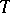 in the variable
in the variable 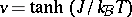 [a7], or Monte-Carlo methods [a8]. It also played a pivotal role for the concepts on surface effects on phase transitions, and for phase coexistence (domains of oppositely oriented magnetization, separated by walls). Such problems were described with a mathematical rigor that is seldomly found in the statistical thermodynamics of many-body systems. Rigorous work includes the existence of a spontaneous magnetization for
[a7], or Monte-Carlo methods [a8]. It also played a pivotal role for the concepts on surface effects on phase transitions, and for phase coexistence (domains of oppositely oriented magnetization, separated by walls). Such problems were described with a mathematical rigor that is seldomly found in the statistical thermodynamics of many-body systems. Rigorous work includes the existence of a spontaneous magnetization for 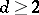 ( "Peierls proof" ), inequalities between spin correlations, theorems on the zeros of the partition function, etc.; see [a9]. The Ising model is the yardstick against which each new approach is measured.
( "Peierls proof" ), inequalities between spin correlations, theorems on the zeros of the partition function, etc.; see [a9]. The Ising model is the yardstick against which each new approach is measured.
Finally, there are extensions of the Ising model. One direction is to make the 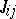 more complicated rather than uniformly ferromagnetic (
more complicated rather than uniformly ferromagnetic (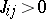 ). E.g., if in one lattice direction
). E.g., if in one lattice direction 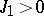 between nearest neighbours but
between nearest neighbours but 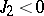 between next nearest neighbours, the resulting anisotropic next nearest neighbour Ising model (ANNNI model) is famous [a10] for its phase diagram with infinitely many phases and transitions; choosing the
between next nearest neighbours, the resulting anisotropic next nearest neighbour Ising model (ANNNI model) is famous [a10] for its phase diagram with infinitely many phases and transitions; choosing the 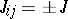 at random from a prescribed distribution, the resulting Ising spin glass [a11] is a prototype model of glasses and other disordered solids.
at random from a prescribed distribution, the resulting Ising spin glass [a11] is a prototype model of glasses and other disordered solids.
Another extension adds "time t" as a variable: by a transition probability 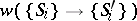 per unit time one is led to a master equation for the probability that a state
per unit time one is led to a master equation for the probability that a state 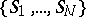 occurs at time
occurs at time 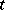 . Such kinetic Ising models [a12] are most valuable to test concepts of non-equilibrium statistical mechanics, and provide the basis for simulations of unmixing in alloys ( "spinodal decomposition" ), etc. Finally, one can generalize the Ising model by replacing the spin
. Such kinetic Ising models [a12] are most valuable to test concepts of non-equilibrium statistical mechanics, and provide the basis for simulations of unmixing in alloys ( "spinodal decomposition" ), etc. Finally, one can generalize the Ising model by replacing the spin 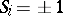 by a more complex variable, e.g. in the Potts model [a13] each site may be in one of
by a more complex variable, e.g. in the Potts model [a13] each site may be in one of 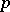 states where
states where 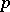 is integer (also, the limit
is integer (also, the limit 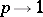 is of interest; the so-called "percolation problem" [a14]). The techniques for the Ising model (transfer matrix, series expansions, renormalization, Monte Carlo, etc.) are valuable for all these related problems, too.
is of interest; the so-called "percolation problem" [a14]). The techniques for the Ising model (transfer matrix, series expansions, renormalization, Monte Carlo, etc.) are valuable for all these related problems, too.
References
| [a1] | E. Ising, "Beitrag zur Theorie des Ferromagnetismus" Z. Phys. , 31 (1925) pp. 253–258 |
| [a2] | L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1958) |
| [a3] | R.J. Baxter, "Exactly solved models in statistical mechanics" , Acad. Press (1982) |
| [a4] | L. Onsager, "Crystal statistics I. A two-dimensional model with an order-disorder transition" Phys. Rev. , 65 (1944) pp. 117–149 |
| [a5] | B.M. McCoy, T.T. Wu, "The two-dimensional Ising model" , Harvard Univ. Press (1973) |
| [a6] | M.E. Fisher, "The renormalization group in the theory of critical behavior" Rev. Mod. Phys. , 46 (1974) pp. 597–616 |
| [a7] | "Phase Transitions and Critical Phenomena" C. Domb (ed.) M.S. Green (ed.) , 3 , Acad. Press (1974) |
| [a8] | "Monte Carlo methods in statistical physics" K. Binder (ed.) , Springer (1979) |
| [a9] | R.B. Griffiths, "Rigorous results and theorems" C. Domb (ed.) M.S. Green (ed.) , Phase Transitions and Critical Phenomena , 1 , Acad. Press (1972) pp. 7–109 |
| [a10] | W. Selke, "The Annni model-theoretical analysis and experimental application" Phys. Rep. , 170 (1988) pp. 213–264 |
| [a11] | K. Binder, A.P. Young, "Spin glasses: experimental facts, theoretical concepts, and open questions" Rev. Mod. Phys. , 58 (1986) pp. 801–976 |
| [a12] | K. Kawasaki, "Kinetics of Ising models" C. Domb (ed.) M.S. Green (ed.) , Phase Transitions and Critical Phenomena , 2 , Acad. Press (1972) pp. 443–501 |
| [a13] | F.Y. Wu, "The Potts model" Rev. Mod. Phys. , 54 (1982) pp. 235–268 |
| [a14] | D. Stauffer, A. Aharony, "Introduction to percolation theory" , Taylor&Francis (1992) |
Ising model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ising_model&oldid=15668