Irreducible variety
An algebraic variety that is an irreducible topological space in the Zariski topology. In other words, an algebraic variety is irreducible if it cannot be represented as the union of two proper closed algebraic subvarieties. Irreducibility of a scheme is defined similarly. For a smooth (and even a normal) variety the concepts of being irreducible and being connected are the same. Every irreducible variety has a unique generic point (cf. Point in general position).
By analogy with the decomposition of a topological space into irreducible components, any algebraic variety is the union of finitely many irreducible closed subvarieties. The algebraic basis of this representation (which can be expressed more precisely) is the primary decomposition in commutative Noetherian rings.
A product of irreducible varieties over an algebraically closed field is also irreducible. For an arbitrary ground field this is no longer true. The following version of the concept of an irreducible variety is also useful: A variety 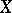 over a field
over a field  is called geometrically irreducible if for any field extension
is called geometrically irreducible if for any field extension 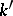 of
of 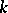 the variety
the variety  obtained from
obtained from 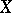 by base change remains irreducible.
by base change remains irreducible.
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Irreducible variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irreducible_variety&oldid=15393