Irreducible polynomial

A polynomial in variables over a field that is a prime element of the ring , that is, it cannot be represented in the form where and are non-constant polynomials with coefficients in (irreducibility over ). A polynomial is called absolutely irreducible if it is irreducible over the algebraic closure of its field of coefficients. The absolutely irreducible polynomials of a single variable are the polynomials of degree 1. In the case of several variables there are absolutely irreducible polynomials of arbitrarily high degree, for example, any polynomial of the form 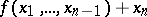is absolutely irreducible.

The polynomial ring 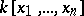is factorial (cf. Factorial ring): Any polynomial splits into a product of irreducibles and this factorization is unique up to constant factors. Over the field of real numbers any irreducible polynomial in a single variable is of degree 1 or 2 and a polynomial of degree 2 is irreducible if and only if its discriminant is negative. Over an arbitrary algebraic number field there are irreducible polynomials of arbitrarily high degree; for example, 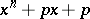, where 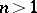and 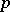is a prime number, is irreducible in 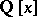by Eisenstein's criterion (see Algebraic equation).

Let 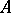be an integrally closed ring with field of fractions and let 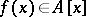be a polynomial in a single variable with leading coefficient 1. If in 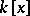and both and 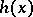have leading coefficient 1, then (Gauss' lemma).

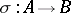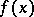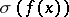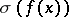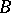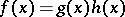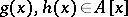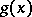Reduction criterion for irreducibility. Let be a homomorphism of integral domains. If and have the same degree and if is irreducible over the field of fractions of , then there is no factorization where and and are not constant. For example, a polynomial 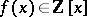with leading coefficient 1 is prime in 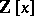(hence irreducible in 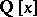) if for some prime 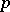the polynomial 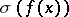obtained from 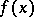by reducing the coefficients modulo is irreducible.

References

[1]	B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German)
[2]	S. Lang, "Algebra" , Addison-Wesley (1974)
[3]	O. Zariski, P. Samuel, "Commutative algebra" , 1–2 , Springer (1975)

Comments

A factorial ring is also known as a unique factorization domain (UFD).