Involutive distribution
The geometric interpretation of a completely-integrable differential system on an  -dimensional differentiable manifold
-dimensional differentiable manifold  of class
of class  ,
,  . A
. A  -dimensional distribution (or a differential system of dimension
-dimensional distribution (or a differential system of dimension  ) of class
) of class  ,
,  , on
, on  is a function associating to each point
is a function associating to each point  a
a  -dimensional linear subspace
-dimensional linear subspace  of the tangent space
of the tangent space  such that
such that  has a neighbourhood
has a neighbourhood  with
with 
 vector fields
vector fields  on it for which the vectors
on it for which the vectors  form a basis of the space
form a basis of the space  at each point
at each point  . The distribution
. The distribution 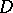 is said to be involutive if for all points
is said to be involutive if for all points 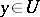 ,
,
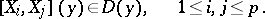 |
This condition can also be stated in terms of differential forms. The distribution  is characterized by the fact that
is characterized by the fact that
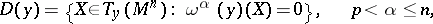 |
where  are
are  -forms of class
-forms of class  , linearly independent at each point
, linearly independent at each point  ; in other words,
; in other words,  is locally equivalent to the system of differential equations
is locally equivalent to the system of differential equations 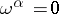 . Then
. Then  is an involutive distribution if there exist
is an involutive distribution if there exist  -forms
-forms  on
on 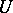 such that
such that
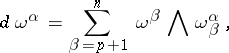 |
that is, the exterior differentials 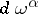 belong to the ideal generated by the forms
belong to the ideal generated by the forms 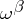 .
.
A distribution  of class
of class  on
on  is involutive if and only if (as a differential system) it is an integrable system (Frobenius' theorem).
is involutive if and only if (as a differential system) it is an integrable system (Frobenius' theorem).
References
| [1] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) |
| [2] | R. Narasimhan, "Analysis on real and complex manifolds" , North-Holland & Masson (1968) (Translated from French) |
Involutive distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Involutive_distribution&oldid=11229