Invertible sheaf
A locally free sheaf of  -modules of rank 1 on a ringed space
-modules of rank 1 on a ringed space 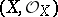 . An equivalent definition is: A sheaf of
. An equivalent definition is: A sheaf of  -modules that is locally isomorphic to the sheaf
-modules that is locally isomorphic to the sheaf 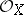 . The invertible sheaves on
. The invertible sheaves on 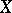 , considered up to isomorphism, form an Abelian group with respect to the operation of tensor multiplication over
, considered up to isomorphism, form an Abelian group with respect to the operation of tensor multiplication over 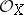 . This group is called the Picard group of the space
. This group is called the Picard group of the space  , and is denoted by
, and is denoted by 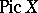 . The inverse of a sheaf
. The inverse of a sheaf  in this group is the sheaf
in this group is the sheaf 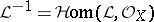 dual to
dual to 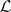 . In the case when
. In the case when 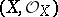 is a scheme (in particular, an algebraic variety) or an analytic space, a sheaf of
is a scheme (in particular, an algebraic variety) or an analytic space, a sheaf of 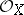 -modules is invertible if and only if it is isomorphic to the sheaf of regular (respectively, analytic) sections of some algebraic (respectively, analytic) line bundle over
-modules is invertible if and only if it is isomorphic to the sheaf of regular (respectively, analytic) sections of some algebraic (respectively, analytic) line bundle over 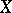 .
.
Invertible sheaves on schemes are closely connected with divisors (cf. Divisor). With each Cartier divisor 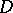 on
on 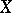 is associated an invertible sheaf
is associated an invertible sheaf 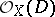 , thus defining an injective homomorphism
, thus defining an injective homomorphism 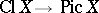 , where
, where 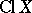 is the group of classes of Cartier divisors on
is the group of classes of Cartier divisors on 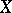 . For integral schemes
. For integral schemes 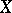 this homomorphism is an isomorphism.
this homomorphism is an isomorphism.
On a projective scheme 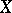 Serre's twisted invertible sheaf
Serre's twisted invertible sheaf 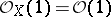 can be defined. In fact, if an imbedding of the scheme
can be defined. In fact, if an imbedding of the scheme 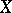 in a projective space
in a projective space 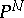 is given, then
is given, then 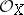 corresponds to the class of a hyperplane section. In particular, if
corresponds to the class of a hyperplane section. In particular, if 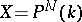 is a projective space over a field
is a projective space over a field 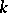 , then the sheaf
, then the sheaf 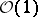 is the direct image of the sheaf of linear functions on
is the direct image of the sheaf of linear functions on 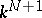 under the natural mapping
under the natural mapping 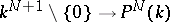 . The system of homogeneous coordinates
. The system of homogeneous coordinates  in
in 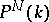 can be identified with a basis for the space of sections
can be identified with a basis for the space of sections 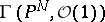 .
.
An invertible sheaf on a scheme 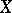 is related to rational mappings of
is related to rational mappings of 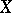 into projective spaces. Let
into projective spaces. Let  be an invertible sheaf on a scheme and let
be an invertible sheaf on a scheme and let 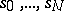 be sections of
be sections of 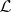 the values of which at any point
the values of which at any point 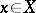 generate the stalk
generate the stalk 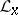 over
over 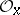 . Then there exists a unique morphism
. Then there exists a unique morphism 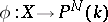 such that
such that 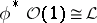 and
and 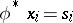 , where
, where 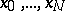 are homogeneous coordinates in
are homogeneous coordinates in 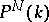 . An invertible sheaf on
. An invertible sheaf on 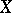 is called very ample if there exists an imbedding
is called very ample if there exists an imbedding  such that
such that 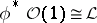 . An invertible sheaf
. An invertible sheaf 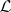 on
on  is called ample if there exists a positive integer
is called ample if there exists a positive integer  for which
for which 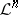 is very ample. On a Noetherian scheme
is very ample. On a Noetherian scheme 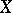 over
over 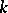 an invertible sheaf
an invertible sheaf 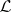 is ample if and only if for each coherent sheaf
is ample if and only if for each coherent sheaf 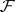 on
on 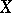 there exists an integer
there exists an integer 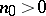 such that the sheaf
such that the sheaf 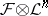 is generated by its global sections for
is generated by its global sections for 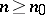 .
.
If 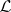 is an ample invertible sheaf on
is an ample invertible sheaf on 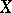 corresponding to a divisor
corresponding to a divisor 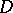 , then
, then 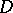 is called an ample divisor. A Cartier divisor
is called an ample divisor. A Cartier divisor 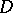 on a scheme
on a scheme 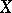 that is proper and smooth over an algebraically closed field
that is proper and smooth over an algebraically closed field 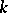 is ample if and only if for each closed integral subscheme
is ample if and only if for each closed integral subscheme 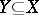 the intersection index
the intersection index 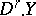 is positive, where
is positive, where  (cf. Intersection index (in algebraic geometry)). For other criteria of ampleness see [5]. There is also a generalization of the concept of an ample divisor on subvarieties of large codimension [2].
(cf. Intersection index (in algebraic geometry)). For other criteria of ampleness see [5]. There is also a generalization of the concept of an ample divisor on subvarieties of large codimension [2].
The concepts of very ample and ample invertible sheaves can be carried over to the case of analytic spaces (for criteria for ampleness in this situation see Positive vector bundle).
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [2] | R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970) |
| [3] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) |
| [4] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [5] | I.V. Dolgachev, "Abstract algebraic geometry" J. Soviet Math. , 2 : 3 (1974) pp. 264–303 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 10 (1972) pp. 47–112 |
Comments
The definition of Serre's twisted invertible sheaf is not precise enough. There is an action of the multiplicative group 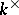 on
on 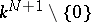 which has
which has 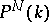 as its quotient. The direct image of the structure sheaf under the mapping
as its quotient. The direct image of the structure sheaf under the mapping 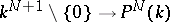 splits into a direct sum of invertible sheaves
splits into a direct sum of invertible sheaves 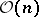 ,
, 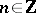 , such that
, such that  acts on
acts on 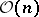 via the character
via the character 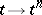 .
.
Invertible sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invertible_sheaf&oldid=12066