Inversion semi-group
inverse semi-group
A semi-group in which any element  possesses a unique inverse element
possesses a unique inverse element 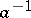 (see Regular element). This property of a semi-group
(see Regular element). This property of a semi-group 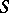 is equivalent to each of the following properties:
is equivalent to each of the following properties: 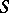 is a regular semi-group and any two of its idempotents commute (thus the set of all idempotents of an inverse semi-group is a semi-lattice, see Idempotents, semi-group of); each left or right principal ideal of
is a regular semi-group and any two of its idempotents commute (thus the set of all idempotents of an inverse semi-group is a semi-lattice, see Idempotents, semi-group of); each left or right principal ideal of 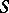 has a unique generating idempotent. Every group is an inverse semi-group; groups are the only inverse semi-groups with a unique idempotent. An important role in the study of inverse semi-groups is played by the following natural partial order relation
has a unique generating idempotent. Every group is an inverse semi-group; groups are the only inverse semi-groups with a unique idempotent. An important role in the study of inverse semi-groups is played by the following natural partial order relation 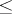 on an arbitrary inverse semi-group
on an arbitrary inverse semi-group 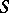 :
: 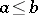 if and only if
if and only if 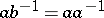 (
(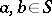 ). On the semi-lattice of idempotents of an inverse semi-group this relation is the same as the natural partial order of this semi-lattice (see Idempotent). A semi-lattice of inverse semi-groups (see Band of semi-groups) is an inverse semi-group. The translation hull of an inverse semi-group (see Translations of semi-groups) is also an inverse semi-group [7]. Every congruence on an inverse semi-group is determined by the classes containing idempotents.
). On the semi-lattice of idempotents of an inverse semi-group this relation is the same as the natural partial order of this semi-lattice (see Idempotent). A semi-lattice of inverse semi-groups (see Band of semi-groups) is an inverse semi-group. The translation hull of an inverse semi-group (see Translations of semi-groups) is also an inverse semi-group [7]. Every congruence on an inverse semi-group is determined by the classes containing idempotents.
Let  be the set of all one-to-one partial transformations of a set
be the set of all one-to-one partial transformations of a set 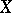 (including the "empty transformation" , taking the empty set to itself). Then
(including the "empty transformation" , taking the empty set to itself). Then 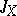 is an inverse semi-group with respect to the operation of superposition, called the symmetric inverse semi-group on
is an inverse semi-group with respect to the operation of superposition, called the symmetric inverse semi-group on 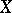 . The following Wagner–Preston theorem is of fundamental importance: Any inverse semi-group
. The following Wagner–Preston theorem is of fundamental importance: Any inverse semi-group 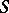 can be isomorphically imbedded in the symmetric inverse semi-group
can be isomorphically imbedded in the symmetric inverse semi-group 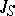 .
.
The theory of inverse semi-groups is an important and deeply researched branch of the theory of semi-groups. Representations of inverse semi-groups by one-to-one partial transformations and matrices over a field have been studied (see [1]). Congruences on inverse semi-groups have been studied. Inverse semi-groups with finiteness conditions are being studied. Quite a number of important special types of inverse semi-groups have been singled out. The restrictions imposed on the majority of these bear the mark of simplicity in some sense (for example, bi-simplicity, see Simple semi-group), or relate to the semi-lattice of idempotents 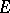 , or are combinations of both types. The restrictions on
, or are combinations of both types. The restrictions on 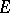 may involve abstract properties of
may involve abstract properties of 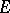 as a semi-lattice (for example, that
as a semi-lattice (for example, that 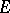 be a certain type of chain) or certain relative properties of
be a certain type of chain) or certain relative properties of 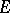 in the semi-group, in particular, the behaviour of
in the semi-group, in particular, the behaviour of 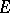 with respect to certain congruences. There exists on any inverse semi-group
with respect to certain congruences. There exists on any inverse semi-group 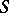 a least congruence
a least congruence 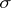 with the property that
with the property that  is a group (the least group congruence), namely
is a group (the least group congruence), namely
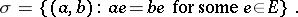 |
An inverse semi-group is called proper if 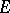 constitutes a
constitutes a 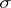 -class. There exists on any inverse semi-group
-class. There exists on any inverse semi-group 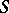 a largest congruence
a largest congruence 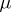 separating idempotents, namely
separating idempotents, namely
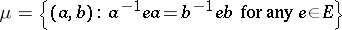 |
and  is contained in the relation
is contained in the relation 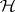 (see Green equivalence relations); an inverse semi-group is called fundamental if
(see Green equivalence relations); an inverse semi-group is called fundamental if 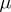 is the same as the equality relation. Quite a number of structure theorems have been obtained for inverse semi-groups of the above-mentioned types, and in many instances the description of inverse semi-groups is effected "modulo groups" ; the groups emerge as blocks of various structures in which semi-lattices, group homomorphisms, etc. also participate. Of this type, for example, are the typical descriptions of Clifford inverse semi-groups (see Clifford semi-group) and the completely
is the same as the equality relation. Quite a number of structure theorems have been obtained for inverse semi-groups of the above-mentioned types, and in many instances the description of inverse semi-groups is effected "modulo groups" ; the groups emerge as blocks of various structures in which semi-lattices, group homomorphisms, etc. also participate. Of this type, for example, are the typical descriptions of Clifford inverse semi-groups (see Clifford semi-group) and the completely 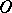 -simple inverse semi-groups (see Brandt semi-group).
-simple inverse semi-groups (see Brandt semi-group).
Inverse semi-groups can also be regarded as universal algebras with two operations: the binary operation of multiplication and the unary operation of taking the inverse element. A classification has been obtained of the monogenic (that is, generated by a single element) inverse semi-groups as universal algebras [6], [9]. With respect to the above operations the class of all inverse semi-groups is a variety; it can be defined, for example, by the following system of identities [8]:
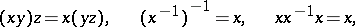 |
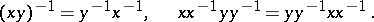 |
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
| [3] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [4] | V.V. Vagner, "Generalized groups" Dokl. Akad. Nauk SSSR , 84 : 6 (1952) pp. 1119–1122 (In Russian) |
| [5] | G.B. Preston, "Inverse semigroups" J. London Math. Soc. , 29 : 4 (1954) pp. 396–403 |
| [6] | L.M. Gluskin, "Elementary generalized groups" Mat. Sb. , 41 : 1 (1957) pp. 23–36 (In Russian) |
| [7] | I.S. Ponizovskii, "Remark on inverse semigroups" Uspekhi Mat. Nauk , 20 : 6 (1965) pp. 147–148 (In Russian) |
| [8] | B.M. Shain, "On the theory of generalized groups and generalized heaps" , The theory of semigroups and its applications , 1 , Saratov (1965) pp. 286–324 (In Russian) |
| [9] | T.I. Ershova, "Monogenic inverse semigroups" Mat. Zap. Ural'sk. Univ. , 8 : 1 (1971) pp. 30–33 (In Russian) |
| [10] | W.D. Munn, "Some recent results on the structure of inverse semigroups" K.W. Folley (ed.) , Semigroups , Acad. Press (1969) pp. 107–123 |
| [11] | L. O'Carroll, "Embedding theorems for proper inverse semigroups" J. of Algebra , 42 (1976) pp. 26–40 |
| [12] | M. Petrich, "Inverse semigroups" , Wiley (1984) |
Inversion semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inversion_semi-group&oldid=42685