Inversion
A transformation taking each point 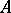 of the plane to the point
of the plane to the point 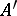 on the ray
on the ray 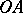 for which
for which 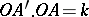 , where
, where 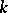 is a constant real number. The point
is a constant real number. The point 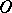 is called the centre, or pole, of the inversion and
is called the centre, or pole, of the inversion and 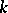 the power, or coefficient, of the inversion. If
the power, or coefficient, of the inversion. If 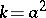 , then points on the circle
, then points on the circle 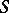 with centre
with centre 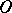 and radius
and radius  are taken to themselves under the inversion; interior points of
are taken to themselves under the inversion; interior points of  are taken to exterior points and vice versa (an inversion is sometimes called a symmetry with respect to a circle). The centre of an inversion does not have an image. An inversion with negative power
are taken to exterior points and vice versa (an inversion is sometimes called a symmetry with respect to a circle). The centre of an inversion does not have an image. An inversion with negative power 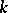 is equivalent to the inversion with the same centre
is equivalent to the inversion with the same centre 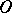 and positive power
and positive power  followed by symmetry in
followed by symmetry in 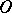 . An inversion with positive power is sometimes called a hyperbolic inversion, while one with negative power is called an elliptic inversion or anti-inversion. A straight line passing through the centre of an inversion is taken into itself under the inversion. A straight line not passing through the centre of an inversion is taken into a circle passing through the centre of the inversion. A circle passing through the centre of an inversion is taken into a straight line not passing through the centre of the inversion. A circle not passing through the centre of an inversion is taken into a circle not passing through the centre of the inversion. In rectangular Cartesian coordinates an inversion can be given by:
. An inversion with positive power is sometimes called a hyperbolic inversion, while one with negative power is called an elliptic inversion or anti-inversion. A straight line passing through the centre of an inversion is taken into itself under the inversion. A straight line not passing through the centre of an inversion is taken into a circle passing through the centre of the inversion. A circle passing through the centre of an inversion is taken into a straight line not passing through the centre of the inversion. A circle not passing through the centre of an inversion is taken into a circle not passing through the centre of the inversion. In rectangular Cartesian coordinates an inversion can be given by:
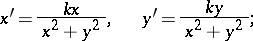 |
and in the complex plane by the formula 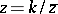 . An inversion is an anti-conformal mapping, that is, it preserves angles between lines and changes their orientation. An inversion in space is defined in a similar way.
. An inversion is an anti-conformal mapping, that is, it preserves angles between lines and changes their orientation. An inversion in space is defined in a similar way.
An inversion is sometimes defined as a mapping of the plane that associates with each point 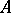 distinct from the centre of a given pencil of circles the point of intersection
distinct from the centre of a given pencil of circles the point of intersection 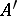 of the circles of the pencil passing through
of the circles of the pencil passing through 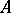 .
.
References
| [1] | P.S. Alexandroff [P.S. Aleksandrov] (ed.) et al. (ed.) , Enzyklopaedie der Elementarmathematik , 4. Geometrie , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
Sometimes an ideal point 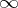 is regarded as the image of the centre of an inversion under this inversion, especially when one considers the inversion on the extended complex plane
is regarded as the image of the centre of an inversion under this inversion, especially when one considers the inversion on the extended complex plane 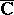 .
.
References
| [a1] | H. Schwerdtfeger, "Geometry of complex numbers" , Dover, reprint (1979) |
| [a2] | D. Pedoe, "Circles" , Pergamon (1957) |
Inversion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inversion&oldid=14957