Inverse scattering, multi-dimensional case
There are many multi-dimensional inverse scattering problems. Below, inverse potential scattering and inverse geophysical scattering are briefly discussed; see Obstacle scattering for inverse obstacle scattering problems.
Inverse potential scattering.
To formulate the inverse potential scattering problem, consider first the direct scattering problem (see [a1], [a2], [a4], [a5], [a6], Appendix):
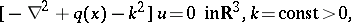 | (a1) |
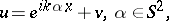 | (a2) |
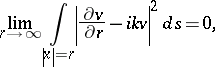 | (a3) |
where 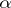 is given,
is given, 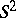 is the unit sphere,
is the unit sphere,  is the scattered field,
is the scattered field,  is the scattering solution, condition (a3) is called the (outgoing) radiation condition,
is the scattering solution, condition (a3) is called the (outgoing) radiation condition, 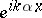 is the incident plane wave, and
is the incident plane wave, and 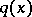 is a real-valued function, called a potential,
is a real-valued function, called a potential,
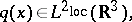 |
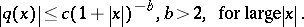 |
The existence and uniqueness of the solution to (a1)–(a3) has been proved under less restrictive assumptions on 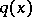 [a2]. The function
[a2]. The function  has the form
has the form
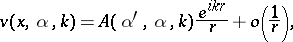 |
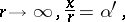 |
where the coefficient 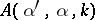 is called the scattering amplitude.
is called the scattering amplitude.
The inverse potential scattering problem consists of finding 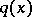 given
given 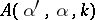 on some subsets of
on some subsets of 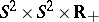 .
.
The first result is simple: If 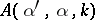 is known for all
is known for all 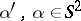 and all
and all 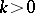 , then
, then  is uniquely determined.
is uniquely determined.
If
 |
then it is known (e.g. [a6], p. 233, see also [a4]) that
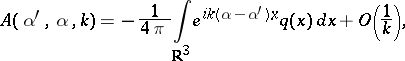 |
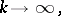 |
so that 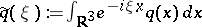 can be found:
can be found:
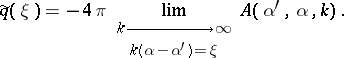 |
The second result is much more difficult.
For decades it was not known if the data 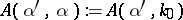 ,
, 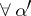 ,
, 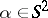 and
and 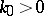 fixed, determine
fixed, determine 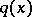 uniquely. In 1987 the uniqueness result has been established by A.G. Ramm (see [a7], [a8]) under the assumptions
uniquely. In 1987 the uniqueness result has been established by A.G. Ramm (see [a7], [a8]) under the assumptions 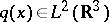 ,
, 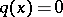 for
for 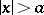 , where
, where  is an arbitrary large fixed number, and in 1988 inversion procedures were published; see [a7]. One of them, proposed by Ramm, is based on the formula
is an arbitrary large fixed number, and in 1988 inversion procedures were published; see [a7]. One of them, proposed by Ramm, is based on the formula
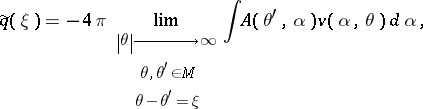 |
where 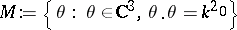 ,
, 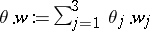 ,
, 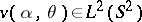 , and
, and 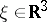 is an arbitrary point.
is an arbitrary point.
Another inversion procedure ([a3], [a7]) is based on the reconstruction of the Dirichlet-to-Neumann mapping and then finding 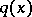 .
.
Error estimates for Ramm's inversion procedure in the case of noisy data and an algorithm for calculating the function 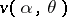 in the inversion formula are obtained in [a9].
in the inversion formula are obtained in [a9].
The uniqueness problem for inverse potential scattering with the data 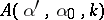 ,
, 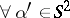 ,
,  ,
, 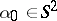 , fixed, is still open (as of 2000).
, fixed, is still open (as of 2000).
The same is true for the uniqueness problem for inverse potential scattering with the (backscattering) data  ,
, 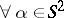 ,
, 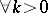 , although for this problem a uniqueness theorem for small
, although for this problem a uniqueness theorem for small 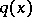 holds.
holds.
Inverse geophysical scattering.
The inverse geophysical scattering problem consists of finding the unknown coefficient 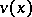 in the equation
in the equation
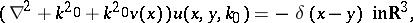 | (a4) |
where 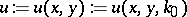 satisfies the outgoing radiation condition (a3),
satisfies the outgoing radiation condition (a3), 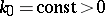 is fixed, and
is fixed, and 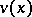 is a real-valued
is a real-valued 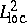 function with compact support in
function with compact support in 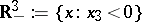 .
.
The scattering data are the values  ,
,  , that is, the values of
, that is, the values of  on the surface of the Earth. The function
on the surface of the Earth. The function  describes an inhomogeneity in the velocity profile (in the refraction coefficient),
describes an inhomogeneity in the velocity profile (in the refraction coefficient),  can be an acoustic pressure. Uniqueness of the solution to inverse geophysical scattering problem was proved in 1987 [a8], [a7].
can be an acoustic pressure. Uniqueness of the solution to inverse geophysical scattering problem was proved in 1987 [a8], [a7].
The uniqueness problem for inverse geophysical scattering with data 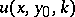 ,
, 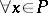 ,
, 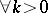 , and
, and 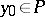 fixed, is open (as of 2000).
fixed, is open (as of 2000).
A reduction of the inverse geophysical scattering problem with the data 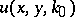 ,
, 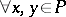 , to the inverse potential scattering problem with the data
, to the inverse potential scattering problem with the data 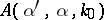 ,
, 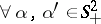 ,
, 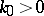 fixed,
fixed, 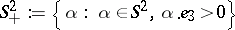 , with
, with 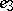 the unit vector along
the unit vector along 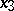 -axis, is done in [a7].
-axis, is done in [a7].
Inverse potential scattering: Open problem.
An interesting open problem (as of 2000) in inverse potential scattering is the problem of finding discontinuities of 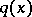 and the number of bound states of the Schrödinger operator generated by the expression
and the number of bound states of the Schrödinger operator generated by the expression 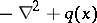 in
in 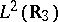 from the knowledge of fixed energy scattering data
from the knowledge of fixed energy scattering data 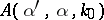 ,
, 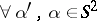 .
.
If 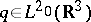 , then
, then 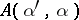 is an analytic function of
is an analytic function of 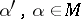 . Therefore, knowledge of
. Therefore, knowledge of 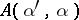 on an open set in
on an open set in 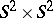 , however small, allows one to recover
, however small, allows one to recover 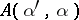 on
on 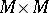 .
.
The assumption concerning compactness of the support of 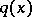 is natural in inverse potential scattering because the scattering data are always noisy and it is not possible in principle to recover the tail of a
is natural in inverse potential scattering because the scattering data are always noisy and it is not possible in principle to recover the tail of a 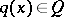 (that is,
(that is,  for
for 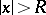 , where
, where  is sufficiently large) from knowledge of noisy data
is sufficiently large) from knowledge of noisy data 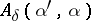 ,
,
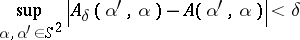 |
(see [a7] for a proof).
References
| [a1] | H. Cycon, R. Froese, W. Kirsch, B. Simon, "Schrödinger operators" , Springer (1986) |
| [a2] | L. Hörmander, "Analysis of linear partial differential operators" , IV , Springer (1985) |
| [a3] | A. Nachman, "Reconstruction from boundary measurements" Ann. Math. , 128 (1988) pp. 531–578 |
| [a4] | R. Newton, "Inverse Schrödinger scattering in three dimensions" , Springer (1989) |
| [a5] | D. Pearson, "Quantum scattering and spectral theory" , Acad. Press (1988) |
| [a6] | A.G. Ramm, "Random fields estimation theory" , Longman/Wiley (1990) |
| [a7] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a8] | A.G. Ramm, "Recovery of the potential from fixed energy scattering data" Inverse Probl. , 4 (1988) pp. 877–886 (See also: Ibid. 3 (1987), L77-82) |
| [a9] | A.G. Ramm, "Stability estimates in inverse scattering" Acta Applic. Math. , 28 : 1 (1992) pp. 1–42 |
| [a10] | A.G. Ramm, "Stability of solutions to inverse scattering problems with fixed-energy data" Rend. Sem. Mat. e Fisico (2001) pp. 135–211 |
Inverse scattering, multi-dimensional case. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_scattering,_multi-dimensional_case&oldid=16465