Difference between revisions of "Inverse scattering, multi-dimensional case"
m (AUTOMATIC EDIT (latexlist): Replaced 93 formulas out of 97 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
m (Automatically changed introduction) |
||
| Line 2: | Line 2: | ||
the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
was used. | was used. | ||
| − | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. |
Out of 97 formulas, 93 were replaced by TEX code.--> | Out of 97 formulas, 93 were replaced by TEX code.--> | ||
| − | {{TEX|semi-auto}}{{TEX| | + | {{TEX|semi-auto}}{{TEX|part}} |
There are many multi-dimensional inverse scattering problems. Below, inverse potential scattering and inverse geophysical scattering are briefly discussed; see [[Obstacle scattering|Obstacle scattering]] for inverse obstacle scattering problems. | There are many multi-dimensional inverse scattering problems. Below, inverse potential scattering and inverse geophysical scattering are briefly discussed; see [[Obstacle scattering|Obstacle scattering]] for inverse obstacle scattering problems. | ||
Revision as of 17:46, 1 July 2020
There are many multi-dimensional inverse scattering problems. Below, inverse potential scattering and inverse geophysical scattering are briefly discussed; see Obstacle scattering for inverse obstacle scattering problems.
Inverse potential scattering.
To formulate the inverse potential scattering problem, consider first the direct scattering problem (see [a1], [a2], [a4], [a5], [a6], Appendix):
\begin{equation} \tag{a1} [ - \nabla ^ { 2 } + q ( x ) - k ^ { 2 } ] u = 0\, \operatorname { in } \mathbf{R} ^ { 3 } ,\, k = \text{const} > 0, \end{equation}
\begin{equation} \tag{a2} u = e ^ { i k \alpha x } + v , \alpha \in S ^ { 2 }, \end{equation}
\begin{equation} \tag{a3} \operatorname { lim } _ { r \rightarrow \infty } \int _ { |x| = r } \left| \frac { \partial v } { \partial r } - i k v \right| ^ { 2 } d s = 0, \end{equation}
where $\alpha$ is given, $S ^ { 2 }$ is the unit sphere, $v$ is the scattered field, $u$ is the scattering solution, condition (a3) is called the (outgoing) radiation condition, $e ^ { i k \alpha x}$ is the incident plane wave, and $q ( x )$ is a real-valued function, called a potential,
\begin{equation*} q ( x ) \in L ^ { 2 }_\text { loc } ( \mathbf{R} ^ { 3 } ), \end{equation*}
\begin{equation*} | q ( x ) | \leq c ( 1 + | x | ) ^ { - b } , b > 2,\text{ for large }|x|. \end{equation*}
The existence and uniqueness of the solution to (a1)–(a3) has been proved under less restrictive assumptions on $q ( x )$ [a2]. The function $v$ has the form
\begin{equation*} v ( x , \alpha , k ) = A ( \alpha ^ { \prime } , \alpha , k ) \frac { e ^ { i k r} } { r } + o \left( \frac { 1 } { r } \right), \end{equation*}
\begin{equation*} r \rightarrow \infty , \frac { x } { r } = \alpha ^ { \prime }, \end{equation*}
where the coefficient $A ( \alpha ^ { \prime } , \alpha , k )$ is called the scattering amplitude.
The inverse potential scattering problem consists of finding $q ( x )$ given $A ( \alpha ^ { \prime } , \alpha , k )$ on some subsets of $S ^ { 2 } \times S ^ { 2 } \times \mathbf{R} _ { + }$.
The first result is simple: If $A ( \alpha ^ { \prime } , \alpha , k )$ is known for all $\alpha ^ { \prime } , \alpha \in S ^ { 2 }$ and all $k > 0$, then $q ( x )$ is uniquely determined.
If
\begin{equation*} q \in Q _ { m } : = \left\{ \begin{array} { c } { q = \overline { q } }, \\ { q : | q ( x ) | + | \nabla ^ { m } q | \leq c ( 1 + | x | ) ^ { - b } }, \\ { b > 3 } \end{array} \right\}, \end{equation*}
then it is known (e.g. [a6], p. 233, see also [a4]) that
\begin{equation*} A ( \alpha ^ { \prime } , \alpha , k ) = - \frac { 1 } { 4 \pi } \int _ { \mathbf{R} ^ { 3 } } e ^ { i k (\alpha - \alpha ^ { \prime } ) x } q ( x ) d x + O \left( \frac { 1 } { k } \right), \end{equation*}
\begin{equation*} k \rightarrow \infty, \end{equation*}
so that $\tilde{q} ( \xi ) : = \int _ { \mathbf{R} ^ { 3 } } e ^ { - i \xi x } q ( x ) d x$ can be found:
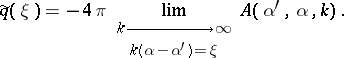 |
The second result is much more difficult.
For decades it was not known if the data $A ( \alpha ^ { \prime } , \alpha ) : = A ( \alpha ^ { \prime } , k _ { 0 } )$, $\forall \alpha ^ { \prime }$, $\alpha \in S ^ { 2 }$ and $k _ { 0 } > 0$ fixed, determine $q ( x )$ uniquely. In 1987 the uniqueness result has been established by A.G. Ramm (see [a7], [a8]) under the assumptions $q ( x ) \in L ^ { 2 } ( \mathbf{R} ^ { 3 } )$, $q ( x ) = 0$ for $| x | > a$, where $a > 0$ is an arbitrary large fixed number, and in 1988 inversion procedures were published; see [a7]. One of them, proposed by Ramm, is based on the formula
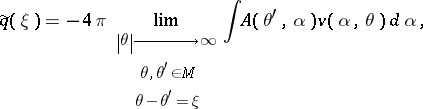 |
where $M : = \left\{ \theta : \theta \in \mathbf{C} ^ { 3 } , \theta . \theta = k ^ { 2_0 } \right\}$, $\theta . w : = \sum _ { j = 1 } ^ { 3 } \theta _ { j } .w _ { j }$, $v ( \alpha , \theta ) \in L ^ { 2 } ( S ^ { 2 } )$, and $\xi \in \mathbf{R} ^ { 3 }$ is an arbitrary point.
Another inversion procedure ([a3], [a7]) is based on the reconstruction of the Dirichlet-to-Neumann mapping and then finding $q ( x )$.
Error estimates for Ramm's inversion procedure in the case of noisy data and an algorithm for calculating the function $v ( \alpha , \theta )$ in the inversion formula are obtained in [a9].
The uniqueness problem for inverse potential scattering with the data $A ( \alpha ^ { \prime } , \alpha_0 , k )$, $\forall \alpha ^ { \prime } \in S ^ { 2 }$, $\forall k > 0$, $\alpha _ { 0 } \in S ^ { 2 }$, fixed, is still open (as of 2000).
The same is true for the uniqueness problem for inverse potential scattering with the (backscattering) data $A ( - \alpha , \alpha , k )$, $\forall \alpha \in S ^ { 2 }$, $\forall k > 0$, although for this problem a uniqueness theorem for small $q ( x )$ holds.
Inverse geophysical scattering.
The inverse geophysical scattering problem consists of finding the unknown coefficient $v ( x )$ in the equation
\begin{equation} \tag{a4} ( \nabla ^ { 2 } + k ^ { 2_0 } + k ^ { 2_0 }v ( x ) ) u ( x , y , k _ { 0 } ) = - \delta ( x - y ) \text { in } \mathbf{R} ^ { 3 }, \end{equation}
where $u : = u ( x , y ) : = u ( x , y , k _ { 0 } )$ satisfies the outgoing radiation condition (a3), $k _ { 0 } = \text { const } > 0$ is fixed, and $v ( x )$ is a real-valued $L _ { \text{loc} } ^ { 2 }$ function with compact support in $\mathbf{R} _ { - } ^ { 3 } : = \{ x : x _ { 3 } < 0 \}$.
The scattering data are the values $u ( x , y )$, $\forall x , y \in P : = \{ x : x_ {3} = 0 \}$, that is, the values of $u$ on the surface of the Earth. The function $v ( x )$ describes an inhomogeneity in the velocity profile (in the refraction coefficient), $u$ can be an acoustic pressure. Uniqueness of the solution to inverse geophysical scattering problem was proved in 1987 [a8], [a7].
The uniqueness problem for inverse geophysical scattering with data $u ( x , y_{0} , k )$, $\forall x \in P$, $\forall k > 0$, and $y _ { 0 } \in P$ fixed, is open (as of 2000).
A reduction of the inverse geophysical scattering problem with the data $u ( x , y , k _ { 0 } )$, $\forall x , y \in P$, to the inverse potential scattering problem with the data $A ( \alpha ^ { \prime } , \alpha , k _ { 0 } )$, $\forall \alpha , \alpha ^ { \prime } \in S _ { + } ^ { 2 }$, $k _ { 0 } > 0$ fixed, $S _ { + } ^ { 2 } : = \left\{ \alpha : \alpha \in S ^ { 2 } , \alpha \cdot e _ { 3 } > 0 \right\}$, with $e_3$ the unit vector along $x _ { 3 }$-axis, is done in [a7].
Inverse potential scattering: Open problem.
An interesting open problem (as of 2000) in inverse potential scattering is the problem of finding discontinuities of $q ( x )$ and the number of bound states of the Schrödinger operator generated by the expression $- \nabla ^ { 2 } + q ( x )$ in $L ^ { 2 } ( \mathbf{R} _ { 3 } )$ from the knowledge of fixed energy scattering data $A ( \alpha ^ { \prime } , \alpha , k _ { 0 } )$, $\forall \alpha ^ { \prime } , \alpha \in S ^ { 2 }$.
If $q \in L ^ { 2_0 } (\mathbf{ R} ^ { 3 } )$, then $A ( \alpha ^ { \prime } , \alpha )$ is an analytic function of $\alpha ^ { \prime } , \alpha \in M$. Therefore, knowledge of $A ( \alpha ^ { \prime } , \alpha )$ on an open set in $S ^ { 2 } \times S ^ { 2 }$, however small, allows one to recover $A ( \alpha ^ { \prime } , \alpha )$ on $M \times M$.
The assumption concerning compactness of the support of $q ( x )$ is natural in inverse potential scattering because the scattering data are always noisy and it is not possible in principle to recover the tail of a $q ( x ) \in Q$ (that is, $q ( x )$ for $| x | > R$, where $R > 0$ is sufficiently large) from knowledge of noisy data $A _ { \delta } ( \alpha ^ { \prime } , \alpha )$,
\begin{equation*} \operatorname { sup } _ { \alpha , \alpha ^ { \prime } \in S ^ { 2 } } | A _ { \delta } ( \alpha ^ { \prime } , \alpha ) - A ( \alpha ^ { \prime } , \alpha ) | < \delta \end{equation*}
(see [a7] for a proof).
References
| [a1] | H. Cycon, R. Froese, W. Kirsch, B. Simon, "Schrödinger operators" , Springer (1986) |
| [a2] | L. Hörmander, "Analysis of linear partial differential operators" , IV , Springer (1985) |
| [a3] | A. Nachman, "Reconstruction from boundary measurements" Ann. Math. , 128 (1988) pp. 531–578 |
| [a4] | R. Newton, "Inverse Schrödinger scattering in three dimensions" , Springer (1989) |
| [a5] | D. Pearson, "Quantum scattering and spectral theory" , Acad. Press (1988) |
| [a6] | A.G. Ramm, "Random fields estimation theory" , Longman/Wiley (1990) |
| [a7] | A.G. Ramm, "Multidimensional inverse scattering problems" , Longman/Wiley (1992) |
| [a8] | A.G. Ramm, "Recovery of the potential from fixed energy scattering data" Inverse Probl. , 4 (1988) pp. 877–886 (See also: Ibid. 3 (1987), L77-82) |
| [a9] | A.G. Ramm, "Stability estimates in inverse scattering" Acta Applic. Math. , 28 : 1 (1992) pp. 1–42 |
| [a10] | A.G. Ramm, "Stability of solutions to inverse scattering problems with fixed-energy data" Rend. Sem. Mat. e Fisico (2001) pp. 135–211 |
Inverse scattering, multi-dimensional case. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inverse_scattering,_multi-dimensional_case&oldid=50828