Invariant differential operator
A differential operator that does not change its form under certain transformations of the space on which it is defined. For example, if  is a partial differential operator written out in some coordinate system
is a partial differential operator written out in some coordinate system  , if
, if  ,
,  , is some transformation of coordinates inducing a corresponding mapping
, is some transformation of coordinates inducing a corresponding mapping  in the set of functions
in the set of functions  (each function
(each function  is associated in a natural way with the function
is associated in a natural way with the function  ) and if
) and if
 |
where the operator 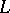 on the right-hand side is expressed in terms of
on the right-hand side is expressed in terms of 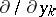 in the same way as the operator
in the same way as the operator 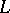 on the left-hand side is expressed in terms of
on the left-hand side is expressed in terms of 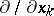 , then
, then 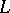 is said to be invariant under the transformation
is said to be invariant under the transformation  (or
(or 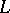 is said to commute with the operator transformation
is said to commute with the operator transformation 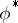 ). The most important case is when a differential operator is invariant under a family of transformations forming a group. The definition of an invariant differential operator becomes substantially more complicated if one considers a system of functions transformed by some representation of this group of transformations. The invariant differential operators related to the Lorentz group and the orthogonal group (the wave operator, the Klein–Gordon and Laplace operators, etc.) play an important role in mathematical physics. In analysis on differentiable manifolds one extensively uses the operator of exterior differentiation
). The most important case is when a differential operator is invariant under a family of transformations forming a group. The definition of an invariant differential operator becomes substantially more complicated if one considers a system of functions transformed by some representation of this group of transformations. The invariant differential operators related to the Lorentz group and the orthogonal group (the wave operator, the Klein–Gordon and Laplace operators, etc.) play an important role in mathematical physics. In analysis on differentiable manifolds one extensively uses the operator of exterior differentiation 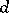 , which is invariant under diffeomorphisms, and the operator
, which is invariant under diffeomorphisms, and the operator  , metrically dual to it, which is invariant under smooth transformations that preserve the metric tensor. In the theory of Lie groups, the so-called left- and right-invariant operators under the corresponding shifts on the group are of great importance.
, metrically dual to it, which is invariant under smooth transformations that preserve the metric tensor. In the theory of Lie groups, the so-called left- and right-invariant operators under the corresponding shifts on the group are of great importance.
References
| [1] | I.G. Petrovskii, "Partial differential equations" , Saunders (1967) (Translated from Russian) |
| [2] | M.A. Naimark, "Les répresentations linéaires du groupe de Lorentz" , Dunod (1962) (Translated from Russian) |
| [3] | G. de Rham, "Differentiable manifolds" , Springer (1984) (Translated from French) |
| [4] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Invariant differential operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariant_differential_operator&oldid=13536