Interval estimator
for the unknown true value of a scalar parameter of a probability distribution
An interval belonging to the set of admissible values of the parameters, with boundaries that are functions of the results of observations subject to the given distribution. Let  be a random variable taking values in a sample space
be a random variable taking values in a sample space  ,
,  ,
,  an interval on the real axis, where the true value of
an interval on the real axis, where the true value of  is unknown. An interval
is unknown. An interval  with boundaries that are functions of the random variable
with boundaries that are functions of the random variable  being observed is called an interval estimator, or confidence interval, for
being observed is called an interval estimator, or confidence interval, for  ; the number
; the number
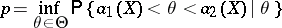 |
is called the confidence coefficient of this confidence interval, and  and
and 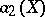 are called the lower, respectively, upper, confidence bounds. The concept of an interval estimator has been generalized to the more general case when it is required to estimate some function, or some value of it, depending on a parameter
are called the lower, respectively, upper, confidence bounds. The concept of an interval estimator has been generalized to the more general case when it is required to estimate some function, or some value of it, depending on a parameter  .
.
Suppose that on a set 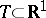 a family of functions
a family of functions
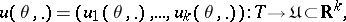 |
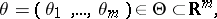 |
has been given, and suppose that it is required to estimate the function 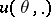 corresponding to the unknown true value of
corresponding to the unknown true value of 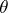 using the realization of a random vector
using the realization of a random vector  taking values in the sample space
taking values in the sample space 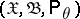 ,
,  ,
, 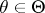 . To each
. To each 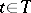 corresponds a set
corresponds a set 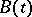 , which is the image of
, which is the image of 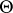 under
under 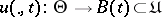 . By definition, a set
. By definition, a set 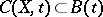 is called a confidence set for
is called a confidence set for 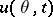 if
if  at
at 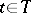 has confidence probability
has confidence probability
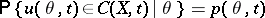 |
and confidence coefficient
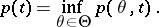 |
The totality of all confidence sets  forms in
forms in 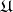 the confidence region
the confidence region 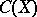 for
for 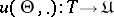 with confidence probability
with confidence probability
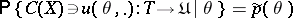 |
and confidence coefficient
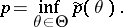 |
Sets of the type  or
or  are called interval estimators for one value
are called interval estimators for one value 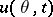 of a function
of a function  at a point and for the function
at a point and for the function 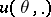 , respectively.
, respectively.
There are several approaches to the construction of interval estimators for independent parameters of a distribution. The best known are the Bayesian approach, based on the Bayes theorem, Fisher's method, based on the fiducial distribution (for Fisher's method, see [3]–[5]), the Neyman method of confidence intervals ([5], [8], [9]), and the method proposed by L.N. Bol'shev [6].
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | R.A. Fisher, "Statistical methods and scientific inference" , Hafner (1973) |
| [3] | S.N. Bernshtein, "On "fiducial" probabilities of Fisher" Izv. Akad. Nauk SSSR Ser. Mat. , 5 (1941) pp. 85–94 (In Russian) (English abstract) |
| [4] | L.N. Bol'shev, "Criticism on "Bernshtein: On fiducial probabilities of Fisher" " , Colected works of S.N. Bernstein , 4 , Moscow (1964) pp. 566–569 (In Russian) |
| [5] | J. Neyman, "Silver jubilee of my dispute with Fisher" J. Oper. Res. Soc. Japan , 3 : 4 (1961) pp. 145–154 |
| [6] | L.N. Bol'shev, "On the construction of confidence limits" Theor. Probab. Appl. , 10 (1965) pp. 173–177 Teor. Veroyatnost. i Primenen. , 10 : 1 (1965) pp. 187–192 |
| [7] | L.N. Bol'shev, E.A. Loginov, "Interval estimates in the presence of nuisance parameters" Theor. Probab. Appl. , 11 (1966) pp. 82–94 Teor. Veryatnost. i Primenen. , 11 : 1 (1966) pp. 94–107 |
| [8] | J. Neyman, "Fiducial argument and the theory of confidence intervals" Biometrika , 32 : 2 (1941) pp. 128–150 |
| [9] | J. Neyman, "Outline of a theory of statistical estimation based on the classical theory of probability" Philos. Trans. Roy. Soc. London , 236 (1937) pp. 333–380 |
Comments
References
| [a1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
Interval estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interval_estimator&oldid=17171