Interval
See Interval and segment.
A space-time interval is a quantity characterizing the relation between two events separated by a spatial distance and a time duration. In special relativity theory the square of an interval is
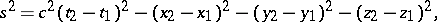 |
where  is the velocity of light,
is the velocity of light,  are the space coordinates and
are the space coordinates and  are the corresponding points in time (for more details, see Minkowski space).
are the corresponding points in time (for more details, see Minkowski space).
In general relativity theory one considers the interval between two infinitesimally-close events:
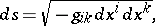 |
where  is the infinitesimal difference of the space-time coordinates of these events and
is the infinitesimal difference of the space-time coordinates of these events and  is the metric tensor.
is the metric tensor.
Comments
A space-time interval with  is called a time-like space-time interval, and one with
is called a time-like space-time interval, and one with  is called a space-like space-time interval.
is called a space-like space-time interval.
References
| [a1] | D.F. Lawden, "An introduction to tensor calculus and relativity" , Methuen (1962) |
| [a2] | R.K. Sachs, H. Wu, "General relativity for mathematicians" , Springer (1977) |
| [a3] | E. Tocaci, "Relativistic mechanics, time, and inertia" , Reidel (1985) pp. Sect. A.II.1.4 |
Interval. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interval&oldid=16796