Intertwining operator
A continuous linear operator 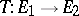 such that
such that 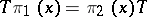 , where
, where 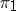 and
and 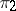 are mappings of a set
are mappings of a set 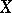 into two topological vector spaces
into two topological vector spaces 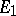 and
and 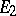 and
and 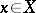 . This concept is especially fruitful in the case when
. This concept is especially fruitful in the case when 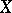 is a group or an algebra and
is a group or an algebra and 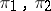 are representations of
are representations of  . The set of intertwining operators forms the space
. The set of intertwining operators forms the space  , which is a subspace of the space of all continuous linear mappings from
, which is a subspace of the space of all continuous linear mappings from 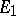 to
to  . If
. If 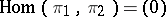 and
and 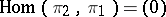 , then
, then 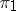 and
and 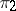 are called disjoint representations. If
are called disjoint representations. If  contains an operator that defines an isomorphism of
contains an operator that defines an isomorphism of 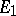 and
and 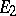 , then
, then 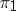 and
and 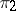 are equivalent. If
are equivalent. If 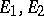 are locally convex spaces, if
are locally convex spaces, if 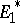 and
and 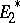 are their adjoints, and if
are their adjoints, and if  and
and 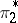 are the representations contragredient to
are the representations contragredient to 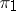 and
and 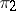 , respectively (cf. Contragredient representation), then for any
, respectively (cf. Contragredient representation), then for any 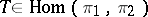 , the operator
, the operator 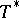 is contained in
is contained in  . If
. If 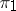 and
and 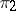 are finite-dimensional or unitary representations and
are finite-dimensional or unitary representations and 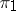 is irreducible, then
is irreducible, then 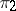 admits a subrepresentation equivalent to
admits a subrepresentation equivalent to 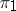 if and only if
if and only if 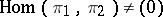 . See also Intertwining number.
. See also Intertwining number.
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | A.I. Shtern, "Theory of group representations" , Springer (1982) (Translated from Russian) |
Intertwining operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intertwining_operator&oldid=47402