Intertwining number
The dimension 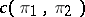 of the space
of the space  of intertwining operators (cf. Intertwining operator) for two mappings
of intertwining operators (cf. Intertwining operator) for two mappings 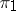 and
and 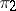 of a set
of a set 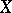 into topological vector spaces
into topological vector spaces 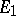 and
and 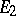 , respectively. The concept of the intertwining number is especially fruitful in the case when
, respectively. The concept of the intertwining number is especially fruitful in the case when 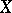 is a group or an algebra and
is a group or an algebra and 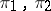 are representations of
are representations of 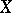 . Even for finite-dimensional representations,
. Even for finite-dimensional representations, 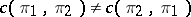 in general, but for finite-dimensional representations
in general, but for finite-dimensional representations 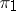 ,
, 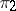 ,
,  the following relations hold:
the following relations hold:
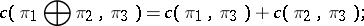 |
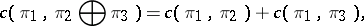 |
while if  is a group, then also
is a group, then also
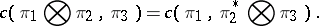 |
If 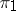 and
and 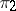 are irreducible and finite dimensional or unitary, then
are irreducible and finite dimensional or unitary, then 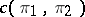 is equal to 1 or 0, depending on whether
is equal to 1 or 0, depending on whether 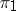 and
and 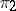 are equivalent or not. For continuous finite-dimensional representations of a compact group, the intertwining number can be expressed in terms of the characters of the representations (cf. also Character of a representation of a group).
are equivalent or not. For continuous finite-dimensional representations of a compact group, the intertwining number can be expressed in terms of the characters of the representations (cf. also Character of a representation of a group).
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | A.I. Shtern, "Theory of group representations" , Springer (1982) (Translated from Russian) |
Intertwining number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intertwining_number&oldid=13682