Intermediate Jacobian
Any of a collection of complex tori determined by the odd-dimensional cohomology spaces of a complex Kähler manifold, and whose geometry is strongly related to the geometry of this manifold.
Let 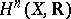 (respectively,
(respectively,  ) be the
) be the  -dimensional cohomology space with real (respectively, integer) coefficients of a complex-analytic Kähler manifold
-dimensional cohomology space with real (respectively, integer) coefficients of a complex-analytic Kähler manifold  . One can introduce a complex structure on the real torus
. One can introduce a complex structure on the real torus
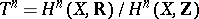 |
if  is odd in two ways, using the representation of the
is odd in two ways, using the representation of the  -dimensional cohomology space with complex coefficients as a direct sum
-dimensional cohomology space with complex coefficients as a direct sum  of the spaces
of the spaces  of harmonic forms of type
of harmonic forms of type 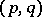 . Let
. Let  be the projections, and let
be the projections, and let
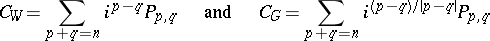 |
be operators mapping the cohomology space with real coefficients into itself. Putting
 |
for any  ,
,  , one obtains two complex structures on
, one obtains two complex structures on  . The first one,
. The first one, 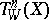 , is called the Weil intermediate Jacobian, and the second,
, is called the Weil intermediate Jacobian, and the second,  , is called the Griffiths intermediate torus. If
, is called the Griffiths intermediate torus. If  is a Hodge variety, then the Hodge metric of
is a Hodge variety, then the Hodge metric of 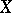 canonically determines on
canonically determines on 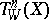 the structure of a polarized Abelian variety (cf. also Polarized algebraic variety; Abelian variety), which is not always true for
the structure of a polarized Abelian variety (cf. also Polarized algebraic variety; Abelian variety), which is not always true for  . On the other hand, holomorphic variation of the manifold
. On the other hand, holomorphic variation of the manifold 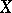 implies holomorphic variation of the intermediate tori
implies holomorphic variation of the intermediate tori 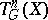 , while Weil intermediate Jacobians need not have this property. The cup-product, giving a pairing between the spaces
, while Weil intermediate Jacobians need not have this property. The cup-product, giving a pairing between the spaces 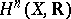 and
and  with
with  , defines a complex pairing of the tori
, defines a complex pairing of the tori 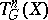 and
and 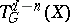 , as well as a duality between the Abelian varieties
, as well as a duality between the Abelian varieties 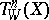 and
and  . If
. If 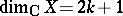 , then
, then  is a self-dual Abelian variety with principal polarization, and
is a self-dual Abelian variety with principal polarization, and 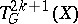 is a principal torus.
is a principal torus.
The intermediate Jacobian is an important invariant of a Kähler manifold. If for two manifolds 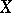 and
and 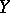 it follows from
it follows from  (or from
(or from 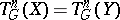 ) that
) that 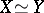 , then one says that Torelli's theorem holds for
, then one says that Torelli's theorem holds for 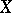 and
and  . Torelli's theorem holds, e.g., for algebraic curves. The irrationality of cubics in the projective space
. Torelli's theorem holds, e.g., for algebraic curves. The irrationality of cubics in the projective space 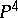 (cf. [1]), as well as that of certain Fano varieties (cf. Fano variety), have been proved by means of the intermediate Jacobian.
(cf. [1]), as well as that of certain Fano varieties (cf. Fano variety), have been proved by means of the intermediate Jacobian.
References
| [1] | C. Clemens, Ph. Griffiths, "The intermediate Jacobian of the cubic threefold" Ann. of Math. , 95 (1975) pp. 281–356 |
| [2a] | Ph. Griffiths, "Periods of integrals on algebraic manifolds I. Construction and properties of the modular varieties" Amer. J. Math. , 90 (1968) pp. 568–626 |
| [2b] | Ph. Griffiths, "Periods of integrals on algebraic manifolds II. Local study of the period mapping" Amer. J. Math. , 90 (1968) pp. 805–865 |
| [3] | A. Weil, "On Picard varieties" Amer. J. Math. , 74 (1952) pp. 865–894 |
Comments
Let  be a complex smooth projective variety and let
be a complex smooth projective variety and let 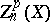 denote the group of algebraic cycles on
denote the group of algebraic cycles on  of codimension
of codimension 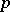 which are homologous to zero (cf. Algebraic cycle). One has the Abel–Jacobi mapping
which are homologous to zero (cf. Algebraic cycle). One has the Abel–Jacobi mapping 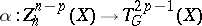 ,
, 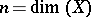 , defined by
, defined by 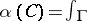 where
where 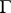 is a
is a  -chain on
-chain on 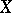 with
with 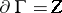 . The image under
. The image under 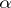 of cycles algebraically equivalent to zero is an Abelian variety. The general Hodge conjecture would imply that this is the maximal Abelian subvariety of
of cycles algebraically equivalent to zero is an Abelian variety. The general Hodge conjecture would imply that this is the maximal Abelian subvariety of 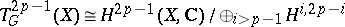 whose tangent space at
whose tangent space at  is contained in
is contained in 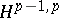 [a1].
[a1].
For an analysis of the behaviour of the Griffiths intermediate Jacobian in a degenerating family see [a2], [a3].
References
| [a1] | D. Lieberman, "Intermediate Jacobians" F. Oort (ed.) , Algebraic geometry (Oslo, 1970) , Wolters-Noordhoff (1972) pp. 125–139 |
| [a2] | S.M. Zucker, "Generalized intermediate Jacobians and the theorem on normal functions" Invent. Math. , 33 (1976) pp. 185–222 |
| [a3] | C.H. Clemens, "The Néron model for families of intermediate Jacobians acquiring "algebraic" singularities" Publ. Math. IHES , 58 (1983) pp. 5–18 |
Intermediate Jacobian. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intermediate_Jacobian&oldid=13065