Interior differential operator

with respect to a surface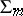

A differential operator 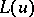such that for any function for which it is defined its value at a point 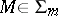can be calculated from only the values of this function on the smooth surface 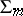defined in the space 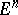, 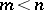. An interior differential operator can be computed using derivatives in directions 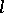which lie in the tangent space to 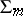. If one introduces coordinates such that on ,

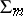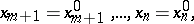then the operator 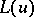, provided it is interior with respect to 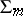, will not contain, after suitable transformations, derivatives with respect to the variables 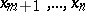(the so-called exterior or extrinsic derivatives). For instance, the operator

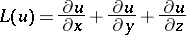is an interior differential operator with respect to any smooth surface containing a straight line 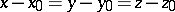, and with respect to any one of these lines. If the operator 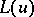is an interior differential operator with respect to a surface 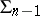, then 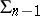is said to be a characteristic of the differential equation .

An operator is sometimes called interior with respect to a surface 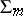if, at the points of this surface, the leading order of the extrinsic derivatives is lower than the order of the operator.