Integrals in involution

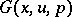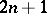Solutions of differential equations whose Jacobi brackets vanish identically. A function of variables 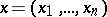, , 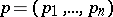is a first integral of the first-order partial differential equation

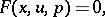(1)

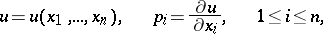if it is constant along each characteristic of this equation. Two first integrals 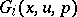, , 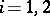are in involution if their Jacobi brackets vanish identically in :

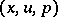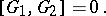(2)

More generally, two functions 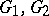are in involution if condition (2) holds. Any first integral 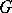of equation (1) is in involution with 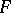; the last function itself is a first integral.

These definitions can be extended to a system of equations

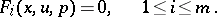(3)

Here the first integral of this system 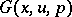can be regarded as a solution of the system of linear equations

(4)

with unknown function .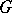

If (3) is an involutional system, then (4) is a complete system. It is in involution if the functions 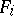in (3) do not depend on .

References

[1]	N.M. Gyunter, "Integrating first-order partial differential equations" , Leningrad-Moscow (1934) (In Russian)
[2]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 2. Partielle Differentialgleichungen erster Ordnung für die gesuchte Funktion , Akad. Verlagsgesell. (1944)

Comments

For additional references see Complete system. An involutional system is usually called a system in involution.