Integral separation condition
From Encyclopedia of Mathematics
A condition on a system of linear differential equations
 |
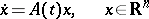(where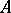 
is a mapping 
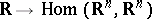with 
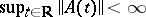), requiring that the system has solutions 
, 
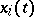, satisfying for certain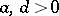 
the inequalities
 |
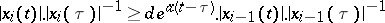for all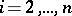 
and all 
.
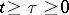The set of systems satisfying the integral separation condition is the interior of the set of continuity of all Lyapunov characteristic exponents (cf. Lyapunov characteristic exponent) in the space of systems
 |
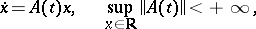with metric
 |
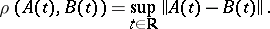References
| [1] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
How to Cite This Entry:
Integral separation condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_separation_condition&oldid=11798
Integral separation condition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_separation_condition&oldid=11798
This article was adapted from an original article by V.M. Millionshchikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article