Integral of a differential equation
A solution of the differential equation. By an integral of a differential equation is primarily meant a relation of the form 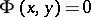 defining a solution
defining a solution 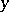 of an ordinary differential equation
of an ordinary differential equation
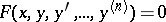 | (1) |
as an implicit function of the independent variable  . The solution is in this case also said to be a particular integral, in contrast to the general integral of equation (1), that is, a relation
. The solution is in this case also said to be a particular integral, in contrast to the general integral of equation (1), that is, a relation
 | (2) |
from which one can obtain by an appropriate choice of the constants 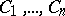 any integral curve of (1) lying in some given region
any integral curve of (1) lying in some given region 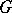 of the
of the 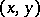 -plane. If the arbitrary constants
-plane. If the arbitrary constants 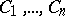 are eliminated from equation (2) and the
are eliminated from equation (2) and the  relations obtained from it by repeated differentiation with respect to
relations obtained from it by repeated differentiation with respect to  (where
(where 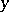 is regarded as a function of
is regarded as a function of  ), then equation (1) results. A relation of the form
), then equation (1) results. A relation of the form
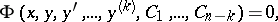 | (3) |
containing derivatives up to order 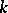 ,
, 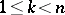 , and
, and  arbitrary constants, arising from the process of integrating equation (1), is sometimes called an intermediate integral of equation (1). If an intermediate integral (3) is known, then the solution of equation (1) of order
arbitrary constants, arising from the process of integrating equation (1), is sometimes called an intermediate integral of equation (1). If an intermediate integral (3) is known, then the solution of equation (1) of order  is reduced to the solution of equation (3) of order
is reduced to the solution of equation (3) of order 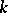 . If (3) contains just one arbitrary constant, that is, if
. If (3) contains just one arbitrary constant, that is, if 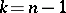 , then it is called a first integral of (1). This equation has exactly
, then it is called a first integral of (1). This equation has exactly  independent first integrals; knowledge of such integrals enables one to obtain the general solution of (1) by eliminating the quantities
independent first integrals; knowledge of such integrals enables one to obtain the general solution of (1) by eliminating the quantities 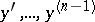 from them.
from them.
If one considers a first-order system of ordinary differential equations,
 | (4) |
then by a general integral of it is meant a set of relations
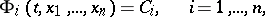 | (5) |
where the  are arbitrary constants, which describes in implicit form all the solutions of the system (4) in some region
are arbitrary constants, which describes in implicit form all the solutions of the system (4) in some region 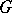 of the
of the 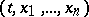 -space. Each of the relations (5) is itself called a first integral of the system (4). More often, by a first integral of the system (4) one means a function
-space. Each of the relations (5) is itself called a first integral of the system (4). More often, by a first integral of the system (4) one means a function  with the property that it is constant along any solution of the system (4) in a region
with the property that it is constant along any solution of the system (4) in a region 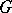 . The system (4) has exactly
. The system (4) has exactly  independent first integrals, knowledge of which enables one to find the general solution without integrating the system; knowledge of
independent first integrals, knowledge of which enables one to find the general solution without integrating the system; knowledge of 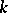 independent first integrals enables one to reduce the solution of the system (4) of order
independent first integrals enables one to reduce the solution of the system (4) of order  to the solution of a system of order
to the solution of a system of order 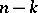 . A smooth function
. A smooth function 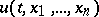 is a first integral of the system (4) with smooth right-hand side if and only if it satisfies the equation
is a first integral of the system (4) with smooth right-hand side if and only if it satisfies the equation
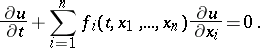 |
Similar terminology is sometimes used in the theory of first-order partial differential equations. Thus, by an integral of the differential equation
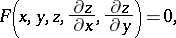 | (6) |
or by a particular integral of it, is meant a solution of this equation (an integral surface). By a complete integral of (6) is meant a family of solutions 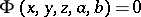 depending on two arbitrary constants. A general integral of equation (6) is a relation containing one arbitrary function and giving a solution of the equation for each choice of this function.
depending on two arbitrary constants. A general integral of equation (6) is a relation containing one arbitrary function and giving a solution of the equation for each choice of this function.
References
| [1] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
References
| [a1] | K. Rektorys (ed.) , Survey of applicable mathematics , Iliffe (1969) pp. Sects. 17.2, 17.8, 17.18, 17.20 |
| [a2] | E.L. Ince, "Integration of ordinary differential equations" , Oliver & Boyd (1956) |
Integral of a differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_of_a_differential_equation&oldid=18935