Integral manifold
A set 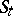 of points of the phase space (
of points of the phase space (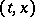 -space) of the system
-space) of the system
 | (*) |
filled by the integral curves of this system (cf. Integral curve), defined for all 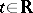 and forming a manifold in
and forming a manifold in 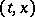 -space. The dimension of the section of
-space. The dimension of the section of 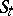 by the plane
by the plane 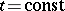 is usually called the dimension of the integral manifold
is usually called the dimension of the integral manifold 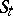 . In the definition of an integral manifold, the requirement that it be a manifold is sometimes replaced by the requirement that the set
. In the definition of an integral manifold, the requirement that it be a manifold is sometimes replaced by the requirement that the set 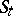 be representable analytically by an equation
be representable analytically by an equation
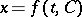 |
with a function 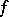 defined for all
defined for all 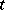 in
in 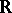 and
and 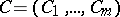 in some domain
in some domain 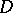 and possessing a specific smoothness in
and possessing a specific smoothness in 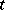 ,
, 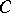 for
for 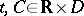 . The integral manifold is then called
. The integral manifold is then called 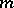 -dimensional and of the same smoothness as the function
-dimensional and of the same smoothness as the function 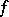 .
.
Examples. An integral curve of a periodic solution of the system (*), that is, a periodic integral curve; the family of integral curves of the system (*) formed by a family of quasi-periodic solutions of (*), filling an 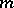 -dimensional torus in the
-dimensional torus in the  -space when
-space when 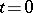 , that is, an
, that is, an  -dimensional toroidal integral manifold; etc.
-dimensional toroidal integral manifold; etc.
The integral manifolds that have been most extensively studied are the toroidal manifolds, that is, sets 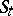 that are tori for any fixed
that are tori for any fixed 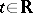 . These manifolds are widely encountered in systems of type (*) describing oscillatory processes.
. These manifolds are widely encountered in systems of type (*) describing oscillatory processes.
References
| [1] | N.N. Bogolyubov, "On certain statistical methods in mathematical physics" , L'vov (1945) (In Russian) |
| [2] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "The method of integral manifolds in non-linear mechanics" , Proc. Internat. Symp. Non-linear Oscillations , 1 , Kiev (1963) pp. 96–154 (In Russian) |
| [3] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "The method of integral manifolds in the theory of differential equations" , Proc. 4-th All-Union Math. Congress (1961) , 2 , Leningrad (1964) pp. 432–437 (In Russian) |
| [4] | N.N. [N.N. Bogolyubov] Bogoliubov, Yu.A. [Yu.A. Mitropol'skii] Mitropoliskii, A.M. [A.M. Samoilenko] Samolenko, "The method of accelerated convergence in non-linear mechanics" , Springer (1976) (Translated from Russian) |
| [5] | Yu.A. Mitropol'skii, "Problems of the asymptotic theory of nonstationary vibrations" , D. Davey (1965) (Translated from Russian) |
| [6] | Yu.A. Mitropol'skii, O.B. Lykova, "Integral manifolds in non-linear mechanics" , Moscow (1973) (In Russian) |
Comments
Nowadays integral manifolds are usually called invariant manifolds. Basic theorems on the permanence of invariant manifolds under perturbations are: 1) Fenichel's theorem, in case the Lyapunov exponents (cf. Lyapunov characteristic exponent) in the directions transversal to the manifold are larger in absolute value than those in directions parallel to the manifold, cf. [a1]; and 2) the Kolmogorov–Arnol'd–Moser theorem on persistence of quasi-periodic solutions in perturbations of integrable Hamiltonian systems (cf. Integrable system; Hamiltonian system; [a2]).
References
| [a1] | M.W. Hirsch, C. Pugh, M. Shub, "Invariant manifolds" , Springer (1977) |
| [a2] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) pp. Appendix 8 (Translated from Russian) |
| [a3] | J. Guckenheimer, P. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983) |
Integral manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_manifold&oldid=17392