Integral logarithm

The special function defined, for positive real , , by

for the integrand has at an infinite discontinuity and the integral logarithm is taken to be the principal value

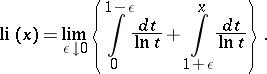The graph of the integral logarithm is given in the article Integral exponential function. For small:

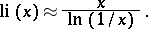The integral logarithm has for positive real the series representation

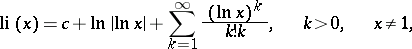where 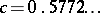is the Euler constant. As a function of the complex variable ,

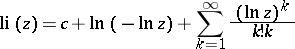is a single-valued analytic function in the complex -plane with slits along the real axis from 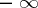to 0 and from 1 to (the imaginary part of the logarithms is taken within the limits 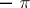and 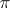). The behaviour of 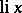along 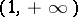is described by

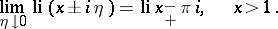The integral logarithm is related to the integral exponential function 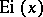by

For real one sometimes uses the notation

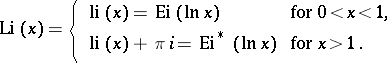For references, see Integral cosine.

Comments

The function 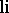is better known as the logarithmic integral. It can, of course, be defined by the integral (as above) for .

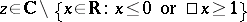The series representation for positive , , 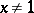is then also said to define the modified logarithmic integral, and is the boundary value of 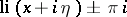, , 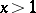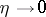. For real 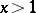the value is a good approximation of , the number of primes smaller than (see de la Vallée-Poussin theorem; Distribution of prime numbers; Prime number).