Integral funnel

of a point for a differential equation

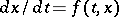
The set of all points lying on the integral curves (cf. Integral curve) passing through 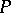. (By an equation one can mean a system of equations in vector notation with 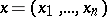.) If only one integral curve passes through 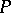, then the integral funnel consists of this single curve. In the case 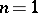, that is, when is scalar, the integral funnel consists of points 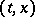for which 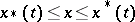, where 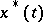and 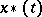are the upper and lower solutions, that is, the largest and smallest solutions passing through .

If the function is continuous (or satisfies the conditions of the Carathéodory existence theorem), then the integral funnel is a closed set. Furthermore, if all the solutions passing through 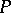exist on the interval 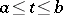, then this segment of the funnel (the part of the integral funnel defined by the inequalities 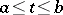) and the section of the integral funnel by any plane 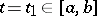are connected compact sets. Any point on the boundary of the integral funnel can be joined to 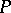by a piece of the integral curve lying on the boundary of the integral funnel. If the sequence of points 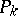, 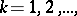converges to 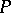, then the segments of the funnels of the points 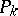converge to the segment of the funnel of 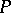in the sense that for any 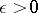they are contained in an -neighbourhood of the segment of the funnel o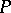f if 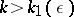. Analogous properties are possessed by integral funnels for differential inclusions (cf. Differential inclusion)

under specified hypotheses concerning the set .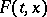

References

[1]	E. Kamke, "Zur Theorie der Systeme gewöhnlicher Differentialgleichungen. II" Acta Math. , 58 (1932) pp. 57–85
[2]	M.F. Bokstein, Uchen. Zap. Moskov. Gos. Univ. Ser. Mat. , 15 (1939) pp. 3–72
[3]	C.C. Pugh, "Funnel sections" J. Differential Eq. , 19 : 2 (1975) pp. 270–295

References

[a1]	A.F. Filippov, "Differential equations with discontinuous righthand sides" , Kluwer (1988) pp. 16 (Translated from Russian)