Integral extension of a ring
An extension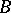 
of a commutative ring 
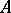with unit element such that every element 
is integral over 
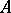, that is, satisfies an equation of the form
 |
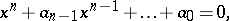where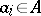 
, a so-called equation of integral dependence.
An element 
is integral over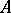 
if and only if one of the following two equivalent conditions is satisfied: 1) 
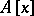is an 
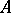-module of finite type; or 2) there exists a faithful 
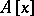-module that is an 
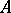-module of finite type. An integral element is algebraic over 
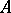. If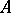 
is a field, the converse assertion holds. Elements of the field 
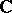of complex numbers that are integral over 
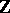are called algebraic integers. If a ring 
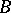is a module of finite type over 
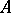, then every element 
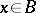is integral over 
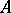(the converse need not be true).
Suppose that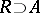 
is a commutative ring, and let 
and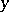 
be elements of 
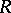that are integral over 
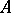. Then 
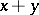and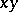 
are also integral over 
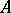, and the set of all elements of 
that are integral over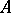 
forms a subring, called the integral closure of 
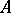in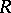 
. All rings considered below are assumed to be commutative.
If 
is integral over 
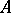and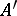 
is some 
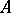-algebra, then 
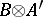is integral over 
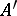. If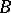 
is an integral extension of 
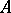and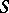 
is some multiplicative subset of 
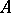, then the ring 
is integral over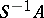 
. An integral domain 
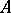is said to be integrally closed if the integral closure of 
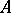in its field of fractions is 
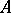. A factorial ring is integrally closed. A ring 
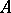is integrally closed if and only if for every maximal ideal 
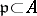the local ring 
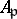is integrally closed.
Let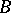 
be an integral extension of 
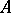and let 
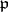be a prime ideal of 
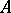. Then 
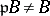and there exists a prime ideal 
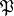of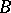 
that lies above 
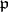(that is, 
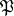is such that 
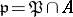). The ideal 
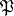is maximal if and only if 
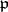is maximal. If 
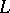is a finite extension of the field of fractions of a ring 
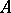and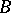 
is the integral closure of 
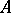in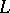 
, then there are only finitely-many prime ideals of 
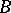that lie above a given prime ideal of 
.
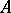Suppose that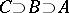 
; then 
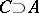is an integral extension if and only if both 
and 
are integral extensions.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
Integral extension of a ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_extension_of_a_ring&oldid=17415