Integral equation with symmetric kernel
An integral equation with a real symmetric kernel (cf. Kernel of an integral operator):
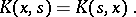 |
The theory of linear equations with real symmetric kernel was first constructed by D. Hilbert (1904) by drawing upon the theory of symmetric quadratic forms and going over from a finite to an infinite number of variables. Shortly after this, E. Schmidt (1907) put forward a more elementary method of substantiating Hilbert's results. For this reason, the theory of integral equations with symmetric kernel is also called the Hilbert–Schmidt theory. A significant weakening of the restrictions imposed in this theory on the data and unknown elements was achieved by T. Carleman (see below).
Consider an integral equation of the second kind with real symmetric kernel:
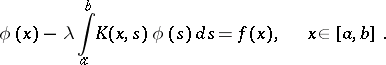 | (1) |
In the construction of the theory of integral equations with symmetric kernel, it suffices to suppose that the symmetric kernel 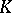 is measurable on the square
is measurable on the square 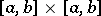 and that
and that
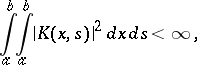 | (2) |
while the free term 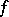 and the unknown function
and the unknown function 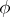 are square-integrable functions on
are square-integrable functions on 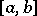 (the integral being understood in the sense of Lebesgue).
(the integral being understood in the sense of Lebesgue).
The development of the theory of integral equations with symmetric kernel begins with the study of a number of general properties of the eigen values and functions of the homogeneous symmetric integral equation
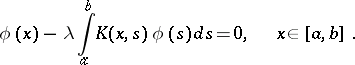 | (3) |
Thus it is proved that: equation (3) has at least one eigen value (when 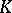 is almost-everywhere non-zero); eigen functions corresponding to distinct eigen values are orthogonal; the eigen values are real; since the kernel is real, it can be assumed without loss of generality that the eigen functions are real; and there are only a finite number of eigen values on any finite interval of values for the parameter
is almost-everywhere non-zero); eigen functions corresponding to distinct eigen values are orthogonal; the eigen values are real; since the kernel is real, it can be assumed without loss of generality that the eigen functions are real; and there are only a finite number of eigen values on any finite interval of values for the parameter 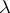 .
.
The set of eigen values of (3) is called the spectrum of the equation. The spectrum is a non-empty finite or countable set of numbers 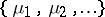 ; to each
; to each 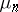 of the spectrum corresponds a finite set of linearly independent eigen functions. The eigen values and eigen functions can be arranged as two sequences:
of the spectrum corresponds a finite set of linearly independent eigen functions. The eigen values and eigen functions can be arranged as two sequences:
 | (4) |
such that the absolute values of the eigen values are non-decreasing: 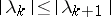 , and each eigen value is repeated as many times as there are eigen functions corresponding to it. Thus, to each
, and each eigen value is repeated as many times as there are eigen functions corresponding to it. Thus, to each 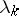 in (4) corresponds just one eigen function. The system of eigen functions
in (4) corresponds just one eigen function. The system of eigen functions 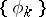 can be assumed to be orthonormal. The sequence (4) is called a system of eigen values and eigen functions (or an eigen system) of the symmetric kernel
can be assumed to be orthonormal. The sequence (4) is called a system of eigen values and eigen functions (or an eigen system) of the symmetric kernel 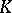 or of the equation (3). The determination of this system is equivalent to the complete solution of the homogeneous symmetric integral equation (3).
or of the equation (3). The determination of this system is equivalent to the complete solution of the homogeneous symmetric integral equation (3).
The Fourier series of the kernel 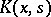 , regarded as a function of
, regarded as a function of  , with respect to the orthonormal system
, with respect to the orthonormal system 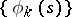 is
is
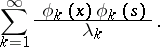 | (5) |
This series formed from the eigen system of the symmetric kernel 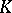 is called the bilinear series of
is called the bilinear series of 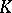 , or the bilinear expansion of
, or the bilinear expansion of  in eigen functions. This series converges in the mean to
in eigen functions. This series converges in the mean to 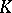 , that is,
, that is,
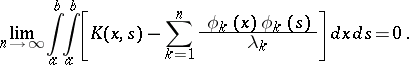 |
If, in addition, the bilinear series (5) converges uniformly, then
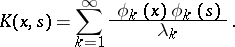 |
In particular, the latter equality always holds if the kernel has only a finite number of eigen values. In this case the kernel 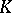 is degenerate (cf. Degenerate kernel).
is degenerate (cf. Degenerate kernel).
The converse statement also holds: A degenerate symmetric kernel has a finite number of eigen values (and, hence, a finite set of eigen functions). The bilinear series of a kernel 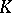 that is continuous on the square
that is continuous on the square 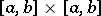 and has positive eigen values converges uniformly.
and has positive eigen values converges uniformly.
Knowledge of the eigen system (4) enables one to construct the solution of the inhomogeneous equation (1). The following theorems hold.
If 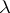 is not an eigen value of
is not an eigen value of 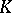 , then the symmetric integral equation (1) has a unique solution
, then the symmetric integral equation (1) has a unique solution 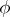 , given by the formula
, given by the formula
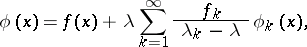 | (6) |
where 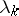 are the eigen values and
are the eigen values and  are the Fourier coefficients of
are the Fourier coefficients of 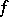 with respect to the orthogonal system
with respect to the orthogonal system 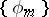 of eigen functions of the kernel, in other words,
of eigen functions of the kernel, in other words,
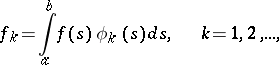 |
Let  be an eigen value of
be an eigen value of 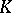 . Then the symmetric integral equation (1) is solvable if and only if the following conditions hold:
. Then the symmetric integral equation (1) is solvable if and only if the following conditions hold:
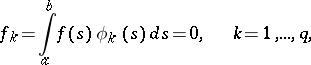 |
where 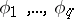 are the eigen functions corresponding to
are the eigen functions corresponding to 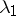 . If these conditions are fulfilled, then all solutions of (1) are expressed by the formula
. If these conditions are fulfilled, then all solutions of (1) are expressed by the formula
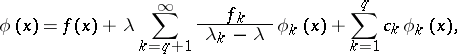 | (7) |
where 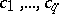 are arbitrary constants.
are arbitrary constants.
If 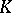 has an infinite number of eigen values and, consequently, there are infinite series on the right-hand sides of the formulas (6), (7), then these series converge in the mean. If it is further required that
has an infinite number of eigen values and, consequently, there are infinite series on the right-hand sides of the formulas (6), (7), then these series converge in the mean. If it is further required that 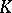 satisfies
satisfies
 |
then the above series converge absolutely and uniformly.
Formulas (6) and (7) are called Schmidt's formulas. Much of the theory of integral equations with symmetric kernel extends easily to complex-valued functions. In this case, the analogue of the real symmetric kernel is a Hermitian kernel: 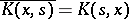 .
.
If the eigen system (4) of a symmetric kernel 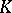 is known, then it is easy to study the symmetric Fredholm equation of the first kind
is known, then it is easy to study the symmetric Fredholm equation of the first kind
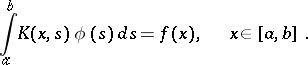 | (8) |
Suppose again that the symmetric kernel 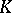 of equation (8) is square integrable on the square
of equation (8) is square integrable on the square 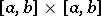 and that the right-hand side
and that the right-hand side 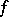 and the unknown function
and the unknown function 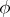 are square-integrable functions on
are square-integrable functions on  .
.
The symmetric kernel is called complete it its system of eigen functions 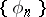 is complete (closed) (cf. Complete system of functions).
is complete (closed) (cf. Complete system of functions).
Picard's theorem. Let 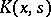 be a complete kernel. Then equation (8) is a solvable if and only if the series
be a complete kernel. Then equation (8) is a solvable if and only if the series
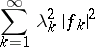 |
converges, where 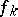 are the Fourier coefficients of
are the Fourier coefficients of 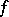 . When the condition holds, the (unique) solution is expressible in the form
. When the condition holds, the (unique) solution is expressible in the form
 | (9) |
and this series converges in the mean.
Carleman [5] has a constructed a theory under less restrictive conditions on the symmetric kernel 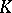 than those of Hilbert and Schmidt. These conditions are as follows: 1)
than those of Hilbert and Schmidt. These conditions are as follows: 1) 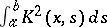 exists in the sense of Lebesgue and
exists in the sense of Lebesgue and
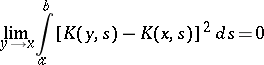 |
for any  , where
, where 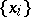 is some sequence of points which may have a finite number of limit points; 2) there may exist a finite set of points
is some sequence of points which may have a finite number of limit points; 2) there may exist a finite set of points 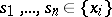 in a neighbourhood of which the function
in a neighbourhood of which the function
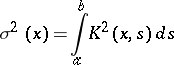 |
is not integrable, but it must be integrable on the set 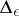 obtained by removing from the interval
obtained by removing from the interval 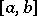 the intervals
the intervals 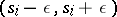 ,
, 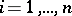 , where
, where  is an arbitrarily small positive number.
is an arbitrarily small positive number.
Let 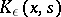 be the function that vanishes on the set of points
be the function that vanishes on the set of points 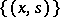 for which
for which 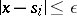 ,
,  ,
,  , and that is equal to the kernel
, and that is equal to the kernel 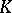 of equation (1) on the set of points of
of equation (1) on the set of points of 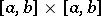 outside this set. The idea of Carleman's method is as follows:
outside this set. The idea of Carleman's method is as follows:
Instead of equation (1) one considers the linear integral equation of the second kind with kernel 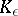 . One studies the spectrum and solutions of this equation and then one investigates the spectrum and solution of equation (1) by passing to the limit as
. One studies the spectrum and solutions of this equation and then one investigates the spectrum and solution of equation (1) by passing to the limit as 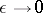 .
.
References
| [1] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) |
| [2a] | E. Schmidt, "Zur Theorie der linearen und nichtlinearen Integralgleichungen. 1. Entwicklung willküriger Funktionen nach Systeme vorgeschriebener" Math. Ann. , 63 (1907) pp. 433–476 |
| [2b] | E. Schmidt, "Zur Theorie der linearen und nichtlinearen Integralgleichungen. 2. Auflösung der allgemeinen linearen Integralgleichung" Math. Ann. , 64 (1907) pp. 162–174 |
| [2c] | E. Schmidt, "Zur Theorie der linearen und nichtlinearen Integralgleichungen. 3. Ueber die Auflösung der nichtlinearen Integralgleichung und die Verzweigung ihrer Lösungen" Math. Ann. , 65 (1908) pp. 370–399 |
| [3] | G. Wiarda, "Integralgleichungen unter besonderer Berücksichtigung der Anwendungen" , Teubner (1930) |
| [4] | S.G. Mikhlin, "Linear integral equations" , Hindushtan Publ. Comp. , Delhi (1960) (Translated from Russian) |
| [5] | T. Carleman, "Sur les équations intégrales singulières à noyau réel et symmétrique" Univ. Årsskrift : 3 , Uppsala (1923) |
Comments
The fact that the bilinear series of a continuous kernel on 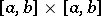 with positive eigen values converges uniformly is usually called the Mercer theorem.
with positive eigen values converges uniformly is usually called the Mercer theorem.
Formula (9) shows the ill-posedness of an integral equation of the first kind: Since 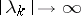 as
as 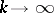 , an arbitrarily small error in
, an arbitrarily small error in 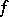 can result in an arbitrarily large error in
can result in an arbitrarily large error in 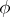 , if it appears in a Fourier component
, if it appears in a Fourier component 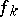 with sufficiently large
with sufficiently large 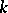 (see Ill-posed problems).
(see Ill-posed problems).
For additional references see Integral equation. See also Hermitian kernel for the symmetricity condition.
References
| [a1] | T. Carleman, "Sur la théorie des équations intégrales et ses applications" , Verh. Internat. Mathematiker Kongress. Zürich, 1932 , 1 , O. Füssli (1932) pp. 138–151 |
| [a2] | E. Tricomi, "Integral equations" , Interscience (1985) |
Integral equation with symmetric kernel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_equation_with_symmetric_kernel&oldid=15316