Integral equation of convolution type
An integral equation containing the unknown function under the integral sign of a convolution transform (see Integral operator). The peculiarity of an integral equation of convolution type is that the kernel of such an equation depends on the difference of the arguments. The simplest example is the equation
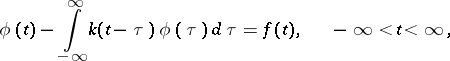 | (1) |
where 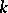 and
and 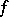 are given functions and
are given functions and 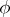 is the unknown function. Suppose that
is the unknown function. Suppose that 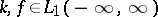 and that one seeks a solution in the same class. In order that (1) is solvable it is necessary and sufficient that the following condition holds:
and that one seeks a solution in the same class. In order that (1) is solvable it is necessary and sufficient that the following condition holds:
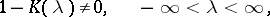 | (2) |
where 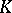 is the Fourier transform of
is the Fourier transform of 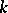 . When (2) holds, equation (1) has a unique solution in the class
. When (2) holds, equation (1) has a unique solution in the class  , representable by the formula
, representable by the formula
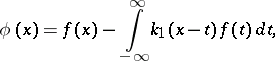 | (3) |
where 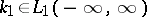 is uniquely determined by its Fourier transform
is uniquely determined by its Fourier transform
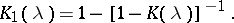 |
An equation of convolution type on the half-line (a Wiener–Hopf equation)
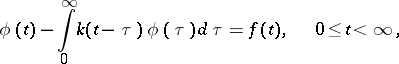 | (4) |
arises in the study of various questions of theoretical and applied character (see [1], [4]).
Suppose that the right-hand side 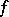 and the unknown function
and the unknown function 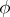 belong to
belong to 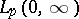 ,
, 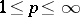 , that the kernel
, that the kernel 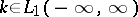 and that
and that
 | (5) |
The function 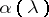 is called the symbol of equation (4). The index of equation (4) is the number
is called the symbol of equation (4). The index of equation (4) is the number
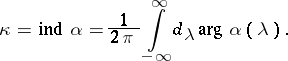 | (6) |
If 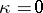 , then the functions
, then the functions  defined by the equations
defined by the equations
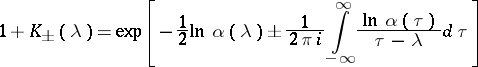 | (7) |
are the Fourier transforms of functions 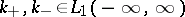 , respectively, such that
, respectively, such that 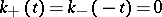 for
for 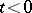 . Under the above conditions, equation (4) has a unique solution, which can be expressed by the formula
. Under the above conditions, equation (4) has a unique solution, which can be expressed by the formula
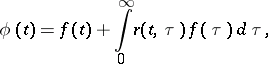 | (8) |
where
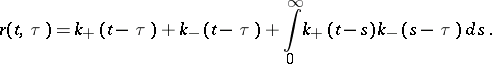 |
If 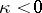 , all solutions of equation (4) are given by the formula
, all solutions of equation (4) are given by the formula
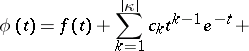 | (9) |
 |
where 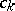 are arbitrary constants,
are arbitrary constants,
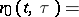 | (10) |
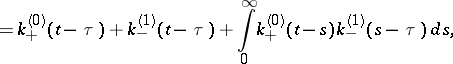 |
and the functions 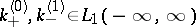 are uniquely determined by their Fourier transforms:
are uniquely determined by their Fourier transforms:
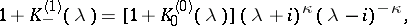 | (11) |
 |
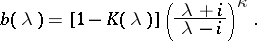 |
When 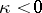 , the homogeneous equation corresponding to (4) has exactly
, the homogeneous equation corresponding to (4) has exactly  linearly independent solutions
linearly independent solutions 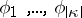 , which are absolutely-continuous functions on any bounded interval; these solutions can be chosen so that
, which are absolutely-continuous functions on any bounded interval; these solutions can be chosen so that  ,
, 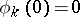 for
for 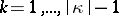 , and
, and 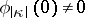 .
.
If 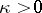 , the equation is solvable only if the following condition holds:
, the equation is solvable only if the following condition holds:
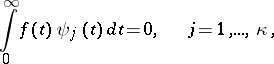 | (12) |
where 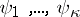 is a system of linearly independent solutions of the transposed homogeneous equation of (4):
is a system of linearly independent solutions of the transposed homogeneous equation of (4):
 | (13) |
Under these conditions, the (unique) solution is given by the formula
 |
where
 |
 |
while the Fourier transforms  and
and  of the functions
of the functions 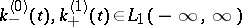 are defined by the equation
are defined by the equation
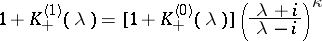 |
and the equations (11). Noether's theorem holds for equation (4) (see Singular integral equation).
The first significant results in the theory of equations (4) were obtained in [11], where an effective method (the so-called Wiener–Hopf method) for solving the homogeneous equation corresponding to (4) was given under the hypothesis that the kernel and the required solution satisfy the conditions: For some 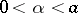 both
both
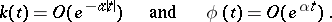 |
The main point of the Wiener–Hopf method is the idea of factorization of a function 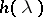 which is holomorphic in the strip
which is holomorphic in the strip 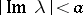 , that is, the possibility to represent it as a product
, that is, the possibility to represent it as a product  , where
, where 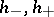 are functions holomorphic in the half-planes
are functions holomorphic in the half-planes 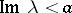 and
and 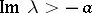 , respectively, and satisfy certain additional requirements. These results have been developed and amplified (see [4]).
, respectively, and satisfy certain additional requirements. These results have been developed and amplified (see [4]).
A method has been developed for reducing equation (4) to a boundary value problem of linear identification. In this way, equation (4) has been solved under the following hypotheses: 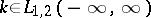 ,
,  ,
, 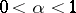 ,
, 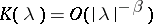 ,
, 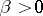 , as
, as  , and
, and  ,
, 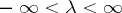 .
.
In addition to this, the role of the number 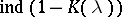 in solving (4) has been clarified. In earlier articles an analogous role was played by the number of zeros of the analytic function
in solving (4) has been clarified. In earlier articles an analogous role was played by the number of zeros of the analytic function 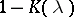 in a strip (see ).
in a strip (see ).
Condition (5) is both necessary and sufficient in order that Noether's theorem holds for equation (4). The solution of equation (4) given above simplifies in a number of particular cases important in practice. The asymptotics of the solution have been obtained for special right-hand sides (see [4]).
Equation (4) has also been studied in the case when 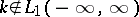 and the Fourier transform
and the Fourier transform 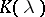 of the kernel
of the kernel 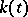 has discontinuities of the first kind (see [5]) or is an almost-periodic function (see [2]). In these cases, condition (5) turns out to be insufficient for Noether's theorem to hold.
has discontinuities of the first kind (see [5]) or is an almost-periodic function (see [2]). In these cases, condition (5) turns out to be insufficient for Noether's theorem to hold.
The validity of the majority of results listed above has also been established for systems of equations of type (4); however, in contrast to the case of a single equation, a system of integral equations of convolution type in the general case cannot be solved explicitly by quadratures (see [6]).
Also related to integral equations of convolution type are paired equations (or dual equations)
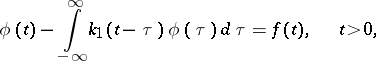 | (15) |
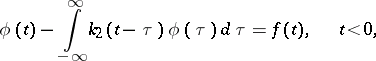 |
and their transposed equations, so-called integral equations of convolution type with two kernels:
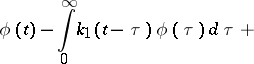 | (16) |
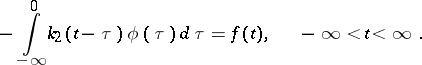 |
Equations (15) have been explicitly solved by quadratures in , and equation (16) in [10].
An integral equation of convolution type on a bounded interval,
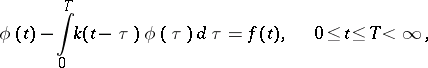 | (17) |
where  , is called a Fredholm equation (see [7], [9]).
, is called a Fredholm equation (see [7], [9]).
Integral equations of convolution type whose symbol vanishes at a finite number of points and the orders of whose zeros are integers, lend themselves to an explicit solution by quadratures (see [8], [12]).
References
| [1] | B. Noble, "Methods based on the Wiener–Hopf technique for the solution of partial differential equations" , Pergamon (1958) |
| [2] | I.C. [I.Ts. Gokhberg] Gohberg, I.A. Feld'man, "Convolution equations and projection methods for their solution" , Transl. Math. Monogr. , 41 , Amer. Math. Soc. (1974) (Translated from Russian) |
| [3a] | I.M. Rapoport, "On a class of singular integral equations" Dokl. Akad. Nauk. SSSR , 59 : 8 (1948) pp. 1403–1406 (In Russian) |
| [3b] | I.M. Rapoport, Trudy Mat. Inst. Steklov. , 12 (1949) pp. 102–117 |
| [4] | M.G. Krein, "Integral equations on the half-line with kernel depending on the difference of the arguments" Uspekhi Mat. Nauk , 13 : 5 (1958) pp. 3–120 (In Russian) |
| [5] | R.V. Duduchava, "Wiener–Hopf integral operators" Math. Nachr. , 65 : 1 (1975) pp. 59–82 (In Russian) |
| [6] | I.Ts. Gokhberg, M.G. Krein, "Fundamental aspects of deficiency numbers, root numbers and indexes of linear operators" Uspekhi Mat. Nauk , 12 : 2 (1957) pp. 44–118 (In Russian) |
| [7] | M.P. Ganin, "On a Fredholm integral equation whose kernel depends on the difference of two arguments" Izv. Vuzov. Mat. : 2 (1963) pp. 31–43 (In Russian) |
| [8] | F.D. Gakhov, V.I. Smagina, "Exceptional cases of integral equations of convolution type and equations of the first kind" Izv. Akad. Nauk SSSR Ser. Mat. , 26 : 3 (1962) pp. 361–390 (In Russian) |
| [9] | I.B. Simonenko, "On some integro-differential equations of convolution type" Izv. Vuzov. Mat. : 2 (1959) pp. 213–226 (In Russian) |
| [10] | Yu.I. Cherskii, "On some special integral equations" Uchen. Zap. Kazansk. Univ. , 113 : 10 (1953) pp. 43–56 (In Russian) |
| [11] | N. Wiener, E. Hopf, "Ueber eine Klasse singulärer Integralgleichungen" Sitz. Ber. Akad. Wiss. Berlin 30/32 (1931) pp. 696–706 |
| [12] | S. Prössdorf, "Einige Klassen singulärer Gleichungen" , Birkhäuser (1974) |
Comments
See also Abel integral equation, for an example.
In general, systems of equations of type (4) cannot be solved explicitly. An exception occurs when the symbol 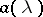 is a rational matrix function. In that case
is a rational matrix function. In that case  can be written in the form
can be written in the form 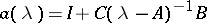 , where
, where 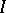 is an identity matrix,
is an identity matrix, 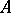 is a square matrix of order
is a square matrix of order 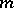 , say, without real eigen values, and
, say, without real eigen values, and  and
and 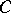 are (possibly non-square) matrices of appropriate sizes. Such a representation, which comes from mathematical systems theory, is called a realization of
are (possibly non-square) matrices of appropriate sizes. Such a representation, which comes from mathematical systems theory, is called a realization of  . The system of Wiener–Hopf equations can now be analyzed in terms of
. The system of Wiener–Hopf equations can now be analyzed in terms of 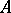 ,
, 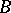 and
and 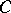 . The analysis yields explicit formulas for solutions, as well as explicit formulas for Wiener–Hopf factorization. Interpreting (4) as a system of equations involving a matrix kernel
. The analysis yields explicit formulas for solutions, as well as explicit formulas for Wiener–Hopf factorization. Interpreting (4) as a system of equations involving a matrix kernel 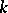 and
and 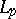 -vector functions
-vector functions 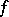 and
and 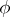 , one of the major results obtained through this approach reads as follows. For each
, one of the major results obtained through this approach reads as follows. For each 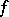 in
in 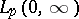 , equation (4) has a unique solution
, equation (4) has a unique solution 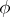 in
in 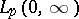 if and only if
if and only if 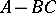 has no real eigen values and
has no real eigen values and 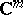 is the direct sum of
is the direct sum of 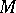 and
and 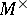 , where
, where 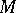 and
and 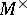 are the spectral subspaces corresponding to the eigen values of
are the spectral subspaces corresponding to the eigen values of 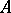 and
and 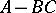 located in the upper and lower half-planes, respectively. Furthermore, in that case the symbol
located in the upper and lower half-planes, respectively. Furthermore, in that case the symbol 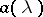 admits a (canonical Wiener–Hopf) factorization
admits a (canonical Wiener–Hopf) factorization 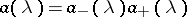 with
with
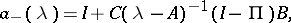 |
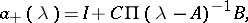 |
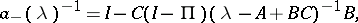 |
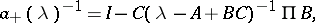 |
and the resolvent kernel 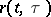 of (4) is given by
of (4) is given by
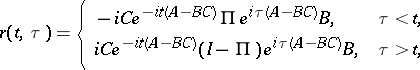 |
where 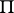 is the projection of
is the projection of 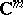 along
along 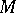 onto
onto 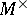 . Of particular interest is the situation where the symbol is self-adjoint (cf. [a11]). For further details and additional results (also on non-canonical Wiener–Hopf factorization) see [a1], [a2], [a7], and [a9]. Generalizations are possible to certain classes of non-rational symbols. For these classes, the realizations involve infinite-dimensional, possibly unbounded, operators (cf. [a3], [a4] and [a9]). For applications to the transport equation and abstract kinetic theory, see [a2], [a8] and [a10]; for applications to
. Of particular interest is the situation where the symbol is self-adjoint (cf. [a11]). For further details and additional results (also on non-canonical Wiener–Hopf factorization) see [a1], [a2], [a7], and [a9]. Generalizations are possible to certain classes of non-rational symbols. For these classes, the realizations involve infinite-dimensional, possibly unbounded, operators (cf. [a3], [a4] and [a9]). For applications to the transport equation and abstract kinetic theory, see [a2], [a8] and [a10]; for applications to 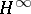 control theory, cf. [a6].
control theory, cf. [a6].
See also Fredholm operator.
References
| [a1] | H. Bart, "Transfer functions and operator theory" Linear Alg. Appl. , 84 (1986) pp. 33–61 |
| [a2] | H. Bart, I. Gohberg, M.A. Kaashoek, "Minimal factorization of matrix and operation functions" , Birkhäuser (1979) |
| [a3] | H Bart, I. Gohberg, M.A. Kaashoek, "Fredholm theory of Wiener–Hopf equations in terms of realization of their symbols" Integr. Eq. Oper. Theory , 8 (1985) pp. 590–613 |
| [a4] | H Bart, I. Gohberg, M.A. Kaashoek, "Wiener–Hopf factorization, inverse Fourier transforms and exponentially dichotomous operators" J. Funct. Anal. , 68 (1986) pp. 1–42 |
| [a5] | K. Clancey, I. Gohberg, "Factorization of matrix functions and singular integral operators" , Birkhäuser (1981) |
| [a6] | B.A. Francis, "A course in 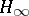 control theory" , Lect. notes in control and inform. science , 88 , Springer (1987) control theory" , Lect. notes in control and inform. science , 88 , Springer (1987) |
| [a7] | I. Gohberg (ed.) M.A. Kaashoek (ed.) , Constructive methods of Wiener–Hopf factorization , Birkhäuser (1986) |
| [a8] | W. Greenberg, C. van der Mee, V. Protopopescu, "Boundary value problems in abstract kinetic theory" , Birkhäuser (1987) |
| [a9] | M.A. Kaashoek, "Minimal factorization, linear systems and integral operators" S.S. Power (ed.) , Operators and function theory , Reidel (1985) pp. 41–86 |
| [a10] | H.G. Kaper, C.G. Lekkerkerker, J. Hejtmanek, "Spectral methods in linear transport theory" , Birkhäuser (1982) |
| [a11] | A.C.M. Ran, "Minimal factorization of selfadjoint rational matrix functions" Integr. Eq. Oper. Theory , 5 (1982) pp. 850–869 |
| [a12] | A.G. Ramm, "Theory and applications of some new classes of integral equations" , Springer (1980) |
| [a13] | A. Ziolkowski, "Deconvolution" , Reidel (1984) |
Integral equation of convolution type. R.V. DuduchavaB.V. Khvedelidze (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_equation_of_convolution_type&oldid=15739