Integral domain
integral ring
A commutative ring with identity and without divisors of zero (cf. Divisor). Any field, and also any ring with identity contained in a field, is an integral domain. Conversely, an integral domain can be imbedded in a field. Such an imbedding is given by the construction of the field of fractions (see Fractions, ring of).
If 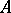 is an integral domain, then the ring of polynomials
is an integral domain, then the ring of polynomials 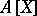 and the ring of formal power series
and the ring of formal power series 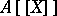 over
over 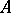 are also integral domains. If
are also integral domains. If 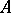 is a commutative ring with identity and
is a commutative ring with identity and 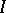 is any ideal in
is any ideal in 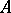 , then the ring
, then the ring 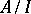 is an integral domain if and only if
is an integral domain if and only if 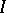 is a prime ideal. A ring
is a prime ideal. A ring 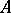 without nilpotents is an integral domain if and only if the spectrum of
without nilpotents is an integral domain if and only if the spectrum of 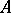 is an irreducible topological space (cf. Spectrum of a ring).
is an irreducible topological space (cf. Spectrum of a ring).
Sometimes commutativity of 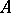 is not required in the definition of an integral domain. Skew-fields and subrings of a skew-field containing the identity are examples of non-commutative integral domains. However, it is not true, in general, that an arbitrary non-commutative integral domain can be imbedded in a skew-field (see [2], and Imbedding of rings).
is not required in the definition of an integral domain. Skew-fields and subrings of a skew-field containing the identity are examples of non-commutative integral domains. However, it is not true, in general, that an arbitrary non-commutative integral domain can be imbedded in a skew-field (see [2], and Imbedding of rings).
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1965) |
| [2] | P.M. Cohn, "Free rings and their relations" , Acad. Press (1985) |
| [3] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
Integral domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_domain&oldid=15894